Die Physik gilt vielen als eine Wissenschaft, die streng kausale Regelmäßigkeiten in der Natur entdeckt und diese als deterministische Naturgesetze in mathematischer Sprache formuliert. In der Tat, die ersten großen Theorien, die in der Geschichte der Physik entstanden, führten zu dieser Vorstellung: Aus ihren Gleichungen kann man eindeutig und in der Praxis auch verlässlich den zukünftigen Zustand eines physikalischen Systems berechnen, wenn man nur die angemessenen Anfangswerte berücksichtigt. Das Funktionieren unserer technischen Geräte bestätigt jeden Tag aufs Neue diese Vorhersagefähigkeit; beim Entgleisen von Zügen oder Abstürzen von Fliegern versagen ja nicht physikalische Gesetze sondern Menschen.

In unserem täglichen Leben aber erfahren wir ständig Unerwartetes und Zufälliges. Unser permanentes Problem ist es, dass wir die Zukunft nicht kennen (auch wenn wir manches Zukünftige gar nicht so genau wissen wollen). Das Unberechenbare gilt als das spezifisch zum menschlichen Leben gehörende und gibt Stoff für viele mehr oder weniger ernste Beziehungsdramen; natürlich ist dabei mit physikalischen Begriffen und Gesetzen nichts auszurichten.

Aber auch schon in der unbelebten Natur gibt es Phänomene, bei denen ein Streben nach exakter Berechenbarkeit völlig absurd wäre, auch wenn man alle grundlegenden Gesetze kennen würde, die bei dem Phänomen eine Rolle spielen. Das hat man im 19. Jahrhundert erkannt, als man die Vorstellung ernst nahm, dass ein Gas aus sich schnell hin und her bewegenden Bausteinen, welcher Art auch immer, besteht und darauf aufbauend versuchte, Beziehungen zwischen dieser Bewegung und den Eigenschaften des Gases herzuleiten. Da sah man sofort ein, dass es nicht sinnvoll sein kann, die Bewegungen aller einzelnen Teilchen mit den Gesetzen der Klassischen Mechanik detailliert zu beschreiben. Die wenigen Eigenschaften eines Gases wie Temperatur oder Druck können sich ja höchstens nur statistisch aus den Positionen und Geschwindigkeiten der “unzähligen” Bausteine ergeben. Man musste somit zu mathematischen Methoden greifen, die im 17. Jahrhundert von Pascal und Fermat erfunden worden waren und heute in den mathematischen Disziplinen “Wahrscheinlichkeitstheorie” und “Mathematische Stochastik und Statistik” gepflegt und weiter entwickelt werden.

Meilensteine dieser Entwicklung zu einer “Statistischen Physik” waren die Überlegungen von Daniel Bernoulli, James Clerk Maxwell und Albert Einstein. Dabei reichte es bei den Fragestellungen von Bernoulli und Maxwell, den Begriff der Wahrscheinlichkeitsverteilung einzuführen, und aus diesen Anfängen entstand zu Beginn des 20. Jahrhunderts die Statistische Mechanik der Gleichgewichtssysteme, die die Beziehungen zwischen den thermodynamischen Eigenschaften von Gasen, Flüssigkeiten und festen Körpern auf die Kräfte zwischen den Bausteinen zurückführen konnte. Aber nicht immer kommt man allein mit Wahrscheinlichkeitsverteilungen aus. So musste Albert Einstein bei seiner Analyse der Brownschen Bewegung schon einen so genannten Zufallsprozess mathematisch formulieren: Betrachtet man Pollen in wässriger Lösung unter dem Mikroskop, so entdeckt man, dass sie in ständiger zittriger Bewegung sind; sie werden ununterbrochen von den Molekülen des Wassers angestoßen. Will man die Bewegung eines Pollens durch eine mathematische Gleichung beschreiben, muss man die Anstöße als eine Krafteinwirkung darstellen, die aber in Größe und Richtung zu jeder Zeit in einer bestimmten Art zufällig ist.

Ich habe die Fragestellungen in der Statistischen Mechanik und bei der Brownschen Bewegung in meinem Artikel “Der Zufall” etwas genauer beschrieben. Hier möchte ich es wagen, näher darauf einzugehen, wie man denn nun allgemein solche Zufallsprozesse mathematisch formuliert. Der Umgang damit und der Gebrauch der dazu notwendigen Konzepte in Anwendungen erfordert einige mathematische Kompetenz, das Prinzip ist aber an einfachen Beispielen leicht zu verstehen. Natürlich spielt dabei der Begriff der Zufallsvariablen eine große Rolle. In dem gerade erwähnten Artikel “Der Zufall” habe ich diesen Begriff schon am Beispiel eines Würfels eingeführt und diesen als “Materialisation” einer bestimmten Zufallsvariablen bezeichnet. Ein Würfel ist ja dadurch gekennzeichnet, dass er beim Würfeln eines von sechs möglichen Ergebnissen liefert, und dass diese dabei alle mit gleicher Wahrscheinlichkeit eintreten können. Eine Zufallsvariable ist nun nichts anderes als ein allgemeinerer, gedachter Würfel: Zu ihrer Definition muss man angeben, welche Werte bei einer Realisierung angenommen werden können und mit welcher Wahrscheinlichkeit dieses jeweils geschehen kann. Im Gegensatz zu einer gewöhnlichen mathematischen Variablen ist eine Zufallsvariable also Platzhalter für mehrere mögliche Werte, und dann muss man also auch sagen, mit welcher Wahrscheinlichkeit diese auftreten, wenn der Variablen ein Wert zugeordnet werden soll. Ich könnte im folgenden also auch immer von einem Würfel reden, wenn ich eine Zufallsvariable meine.

Ein üblicher Würfel mit den möglichen Werten (1,2,3,4,5,6), die alle mit gleicher Wahrscheinlichkeit bei einer Realisierung auftreten, spielt in der Physik keine Rolle, wohl aber z.B. einer, bei dem alle reellen Zahlen zwischen 0 und 1 realisiert werden können und das auch mit gleicher Wahrscheinlichkeit. (Da es hier um ein Kontinuum von Zahlen geht, müsste man bei der Zuordnung von Wahrscheinlichkeiten etwas weiter ausholen, aber das soll uns hier nicht interessieren.) Besonders prominent und häufig nützlich ist eine andere, die “normal verteilte” oder “Gaußsche” Zufallsvariable. Hier kann sich jede reelle Zahl bei einer Realisation ergeben, aber die Wahrscheinlichkeit, dass sich bei der Realisierung eine Zahl eines bestimmten Intervalls ergibt, ist durch “Gaußsche” Glockenkurve (siehe Abb.1) gegeben. Diese besitzt ein bestimmtes Maximum und eine Breite.

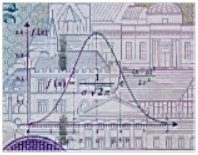
Abb1: 10 DM-Banknote mit dem Konterfei von Carl Friedrich Gauss und Ausschnitt mit dem Graphen einer Gauss-Kurve (rechts), auch Normalverteilung genannt.

Zufallsprozesse kann man nun mathematisch beschreiben, indem man in Gleichungen, die das Zeitverhalten bestimmter Variablen beschreiben sollen, solche gedachten Würfel, d.h. Zufallsvariablen aufnimmt. Bei der Brownschen Bewegung werden die ständigen Stöße so durch eine Zufallskraft modelliert, deren Eigenschaft von der Flüssigkeit abhängt, in denen die Pollen schwimmen. Die mathematischen Gleichungen, die auf diese Weise entstehen, sehen nun zunächst aus wie gewöhnliche Gleichungen, nur dass nun irgendwo ein weiteres Symbol, meistens ein griechischer Buchstabe wie eta oder xi, für eine Zufallsvariable steht.
Was das für die Lösung einer solchen Gleichung bedeutet, kann man schön verfolgen, wenn man die Gleichungen auf einem Rechner lösen will. Man nennt ein solches Lösungsverfahren, wie man bald sehen wird, auch “Simulation”. Für die Zufallsvariable eta oder xi, die Quelle des Zufallscharakters, braucht man dabei einen Zufallsgenerator, also einen Algorithmus, der einem Würfeln gleichkommt und somit, mit der entsprechenden Wahrscheinlichkeit, jeweils einen der möglichen Werte der Zufallszahlen liefert.
Das einfachste Beispiel stellt der so genannte Zufallsweg (random walk) dar. Ein Punkt möge auf einer Linie, sagen wir der x-Achse, wandern können, beginne zu Zeit t=0 bei x=0 und mache zu den Zeiten t=1,2,3, …,N jeweils einen Schritt einer Länge eta(t), wobei eta(t) zu jeder Zeit t eine (unabhängige) Gaußsche Zufallsvariable sei mit einem Maximum bei 0 und einer Breite 0.1. Hier muss man also sogar, um eine Lösung zu erhalten, mehrere Male, d.h. bei jedem Zeitschritt “würfeln”.

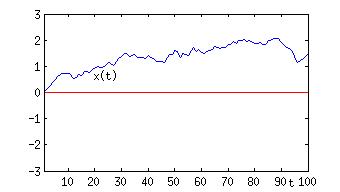
Abb. 2: Zeitreihe einer Realisierung eines so genannten Zufallsweges

In Abb.2 ist solch ein Prozess dargestellt, in dem die Position auf der Ordinate und die Zeit auf der Abszisse abgetragen ist. Man nennt das eine Realisierung des Prozesses, und immer, wenn man den Prozess aus Neue simuliert, also zu Zeiten t=1,2,…. jeweils eine Zufallszahl eta(t)  “auswürfelt”, und x(t+1) = x(t) + eta(t) bildet, erhält man eine andere Realisierung. Trägt man diese alle in dem gleichen Diagramm ein, so erhält man Abb.3. Man sieht deutlich, wie unterschiedlich die Realisierungen sein können. Man hat den Eindruck, dass das Bündel mit der Zeit immer breiter wird. Das ist in der Tat der Fall und es liegt an der Konstruktion des Prozesses. Diese ist aber deswegen nicht als ungeschickt zu betrachten: Eine Schadstoffwolke in der Luft breitet sich auch aus, die Moleküle legen dabei Zufallswege im dreidimensionalen Raum zurück. Allgemein lässt sich jeder diffusive Prozess so modellieren.
Dieses Bild zeigt auch, wie man eine solche Simulation auszuwerten hat. Zu jeder Zeit t erhält man mehrere Realisierungen von x(t). Dieses spiegelt wieder, dass die Lösung solch einer stochastischen Gleichung eigentlich eine Verteilungsfunktion für x(t) für alle Zeiten t=1,2,.. ist. Aus den Realisierungen kann man nun für beliebige Zeiten z.B. Mittelwert und Varianz dieser Verteilung schätzen, und mit zunehmender Anzahl von Realisierungen werden die Schätzwerte für diese Größen genauer werden.

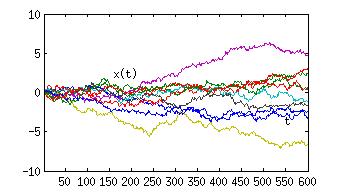
Abb.3: Zeitreihen von 10 Realisierungen eines so genannten Zufallsweges

Die Gleichung für diesen Zufallsweg ist schon genannt worden: x(t+1) = x(t) + eta(t). Sie lässt sich leicht abändern, so dass der Effekt der immer größer werdenden Breite des Bündels von Realisierungen nicht mehr auftritt. Man braucht nur zu schreiben: x(t+1) = a x(t) + eta(t), mit einer Konstanten a < 1, z.B. a=0,9.

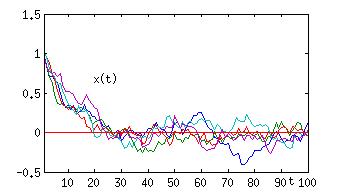
Abb.4: Zeitreihe von Realisierungen eines stochastischen Relaxators.

Wenn man diese Gleichung auf einem Rechner simuliert, dann ergeben sich die in Abb.4 dargestellten Zeitreihen. (Hier beginnt man aber mit x=1, um offensichtlich zu machen, was die Gleichung beschreibt.) Man sieht hier, welche Folgen die Werte von Parametern in einer Gleichung haben können. Auch dieser Prozess beschreibt prototypisch ein wichtiges Phänomen der Natur: Es wird offensichtlich im Mittel ein stationärer Wert, in diesem Falle 0, erreicht, aber es gibt immer noch Fluktuationen um diesen auf die Dauer erreichten Mittelwert. Die Zufallsgröße eta(t) treibt immer wieder das “System” x(t) aus dem Gleichgewicht x=0 heraus, der Zusatz a x(t) mit a<1 sorgt aber dafür, dass x(t) immer wieder zum Gleichgewicht hin getrieben wird. Dieser Prozess ist also ein einfaches Modell für einen so genannten Relaxator, dafür, wie sich ein System in ein (stabiles) Gleichgewicht setzt und darin verharrt. In der Statistik der Fluktuationen um das Gleichgewicht spiegeln sich die Eigenschaften der Störungen eta(t) wieder.
Schließlich darf man es nicht versäumen, noch einen anderen Prozess vorzuführen, der einen auch an viele Phänomene aus dem Leben denken lässt. Bei diesem bestimmt sich die neue Position x(t+1) nicht alleine aus x(t) und eta(t), sondern x(t-1), die Position zur Zeit t-1, soll auch noch eine Rolle spielen. 

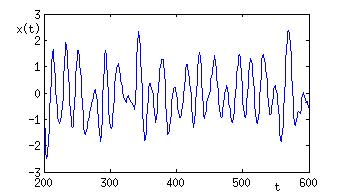
Abb.5: Zeitreihe einer Realisierung eines stochastischen Oszillators

In Abb. 5 sieht man eine Realisation des Prozesses x(t+1) = a x(t) + b x(t-1) + eta(t) (mit a=1.86, b=-0.96). Dieser ist ein Beispiel für einen so genannten stochastischen Oszillator. Die Zeitreihe sieht aus wie ein Abschnitt aus einer digitalen Aufzeichnung eines Musikstückes (z.B. einer wav-Datei), x(t) wäre dann nicht mehr als Position auf einem Weg zu deuten sondern als Schalldruck, den ein Instrument erzeugt hat.
Hiermit haben wir schon die wichtigsten Typen von Zufallsprozessen in Form von Zeitreihen gesehen. Diffusion, Relaxation und Oszillation – das sind drei grundsätzliche Verhaltensmuster, aus denen man sich fast alle Verhaltensweisen zusammengesetzt denken kann. Und in unserer komplexen Welt können wir ständig und überall solche Prozesse beobachten, ob es der Temperaturverlauf bei einer Freiburger Wetterstation ist, das EKG beim Besuch eines Arztes, der Verlauf des Dax an der Börse.
Wir haben also nun eine Vorstellung darüber, wie man auch solche Prozesse, die eben nicht streng deterministisch sind, mathematisch fassen kann. Die Modelle, die ich hier vorgestellt habe, sind aber nur die Spitze eines Eisbergs. Als Methode zur Lösung der Gleichungen habe ich auch nur die Simulation vorgeführt, und die ist bei den vorgestellten Modellen sehr einfach. Wenn man aber erst einmal die Tür zu solchen stochastischen Prozessen geöffnet hat, sieht man bald eine Fülle von Anwendungsmöglichkeiten und es wird plausibel, dass diese mathematische Beschreibung nichtdeterministischer Prozesse nicht nur in der Physik sondern in allen Bereichen der Naturwissenschaft und Technik, ja bei allen quantitativen Analysen auch außerhalb der Naturwissenschaften eine große Rolle spielen. Die vorherrschenden Fragen sind dabei natürlich: Wie findet man das beste Modell für ein beobachtetes Phänomen und wie bestimmt man bei gegebenem Modelltyp die Parameter des Modells? Was kann ich aus solch einem Modell denn dann lernen? Das soll in einem anderen Beitrag beleuchtet werden.