Der Rekordmärz 2013
BLOG: KlimaLounge

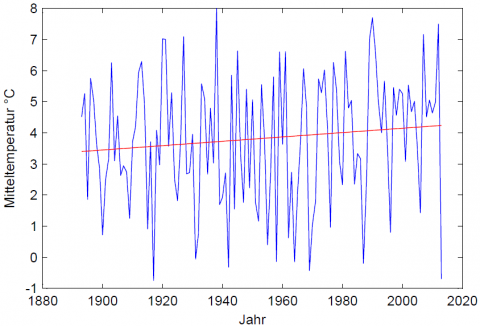
Heute nur ein ganz kurzer Blick auf die Märztemperaturen – wir haben ja in den letzten Beiträgen die Wintertemperaturen in Deutschland und den Zusammenhang von kaltem Wetter bei uns und der Eisschmelze in der Arktis beleuchtet. An unserer Säkularstation Potsdam sieht die Mitteltemperatur für März seit dem Jahr 1893 so aus:
Der vergangene März war mit -0,70 °C nur ganz knapp nicht der kälteste seit Beginn der Messungen; der März 1917 war mit -0,75 °C noch fünf Hundertstel Grad kälter.
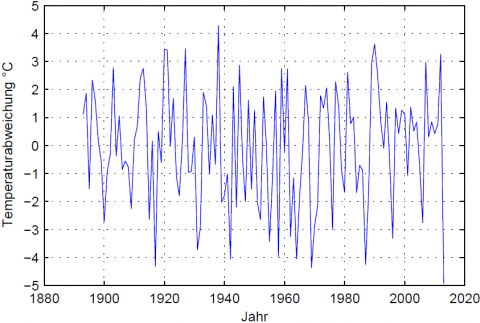
Allerdings sollte noch bedacht werden, dass sich das Klima in den letzten 120 Jahren ja erwärmt hat. Die rote lineare Trendlinie ist eine Möglichkeit, dies zu illustrieren – danach betrug die lineare Erwärmung 0,8 °C. Im Vergleich zu dem insgesamt wärmeren Klima ist dieser März noch ungewöhnlicher. Zieht man den linearen Trend ab, sehen die Märztemperaturen so aus:
Danach wäre der gerade erlebte März sogar mit Abstand der größte Ausreißer nach unten. Er war zudem 8,2 Grad kälter als der März des Vorjahres – die größte Differenz zum Vorjahr, die es sonst in der gesamten Zeitreihe gibt, beträgt 6,3 Grad nach unten bzw. 6,7 Grad im Sprung nach oben. Diese Dinge illustrieren, wie extrem ungewöhnlich die Wetterlage diesen März war – sie lag außerhalb der bisher erlebten normalen Schwankungsbreite des Wetters. Eine mögliche Erklärung haben wir ja im vorigen Beitrag vorgestellt.


Ähm
Also ich weiß nicht, wie Sie aus diesen Zick-Zack-Kurven ausgerechnet diese steigende rote Linie als Trend herauslesen. Bei mir wäre es genau umgekehrt. Ich sehe eher einen sinkenden Trend.
[Antwort: Damit es Wissenschaft und nicht “subjektiver Eindruck” ist, gibt es eine mathematische Standardmethode zur Berechnung des linearen Trends, die hier verwendet wurde. Aber Sie haben einen validen Punkt: die Reihe ist stark “verrauscht”, weshalb ich diese Trendlinie auch nur “eine Möglichkeit” genannt habe, die Klimaerwärmung zu “illustrieren” – sie ist sicher kein schlagender Beweis dafür. Wesentlich deutlicher ist die Erwärmung, wenn Sie z.B. Jahresmitteltemperaturen für ganz Deutschland nehmen, denn die zeigen viel weniger Rauschen als ein Monat an einem Ort. Oder Sie schauen sich gleich die globale Durchschnittstemperatur an – kaum noch Rauschen, und sie zeigt auch 0,8 °C Erwärmung seit Ende des 19. Jahrhunderts. Keinen Zweifel gibt es daran, dass dieser kalte März im Kontext eines deutlich wärmeren Klimas auftrat als der kalte März des Jahres 1917, und daher umso ungewöhnlicher ist. Stefan Rahmstorf]
Hm.
Ich will nicht nerven. Aber ich weiß, dass sehr viele Leute an dieser ganzen Geschichte zweifeln. Ich auch. Zum Beispiel habe ich große Zweifel an der Genauigkeit der Messung. Wir reden hier über fast 300 Grad Kelvin. Da wollen Sie eine Genauikgeit (seit “Ende des 19.Jh.”) von 0,8 Grad haben, was alles in allem eine Änderung i.H.v. 0,26% ausmacht.
Erstens sehe ich da vor dem inneren Auge einen Mann mit Zylinder und Monokel der ein Quecksilberthermometer abliest während draußen Bertha Benz ihre ersten Runden dreht – und darauf fußen ihre Aussagen.
Und zweitens, 0,26% hört sich für mich – und für wer weiß wieviele Millionen alleine in Deutschland – nicht nach der Katastrophe an, die uns immer angedroht wird, sondern genau danach, was man in der Natur erwarten würde: permanenten, unvorhersehbaren Wechsel.
Ich sage es offen: ich denke nicht, dass irgend jemand ausser den Klimatologen überrascht wäre, wenn wir die nächsten 50 Jahre sinkende Temperaturen hätten, und wenn sich herausstellen würde, dass man im Jahre 2013 einfach nicht sicher sagen kann, wie hoch die Temperatur anno 1904 ganz exakt war. Geschweige denn, jemand fragt nach der Temperatur in Sibirien, über den Nordatlantik, dem Pazifik, Zentralafrika, also eigentlich dem Löwenanteil des Planeten – diese Daten werden erst seit kurzem erhoben, soweit ich weiß. Per Satellit.
[Antwort: Zu Ihrem ersten Punkt: es gibt natürlich in der Fachliteratur detaillierte Unsicherheitsanalysen zu den Temperaturmessungen. An der Tatsache der globalen Erwärmung besteht in der Fachwelt keinerlei Zweifel, und ob sie nun 0,7 oder 0,8 oder 0,9 Grad beträgt ändert daran wenig.
Zu Ihrem zweiten Punkt: die Erwärmung als Prozentsatz zum absoluten Nullpunkt der Kelvinskala zu berechnen ergibt keinerlei Anhaltspunkte für die Auswirkungen dieser Erwärmung – oder würden Sie diese Argumentation auch zur Beruhigung anwenden, wenn Ihr Kind 40 Grad Fieber hat? Die Folgen der Erwärmung sind bestens dokumentiert: die Gletscher schwinden weltweit, der Meeresspiegel steigt, der Frühlingsanfang hat sich (mal abgesehen von diesem Jahr) um 1-2 Wochen nach vorn verschoben (was Kirschblüte, Vogelzug etc. angeht), der biologische Herbst kommt entsprechend später, und die Zahl der monatlichen Wärmerekorde hat sich weltweit verfünffacht. Erstaunlich, was 0,8 Grad globale Erwärmung für Folgen haben – wollen Sie wirklich ausprobieren, was die Folgen von 3 oder 4 Grad sein werden? Stefan Rahmstorf]
Monatsmitteltemperatur
Sehr geehrter Herr Professor Rahmsdorf,
schon im letzten Jahr hatte ich mich wegen Ihrer allzu naiven Betrachtung der mittleren Wintertemperaturen für Deutschland an Sie gewandt.
Meine Ermahnung, dass Mittelwerte ohne Angabe von Streuungsmaßen sinnlos sind, haben Sie auch in Ihrem diesjährigen Artikel über die Märztemperaturen ignoriert.
Sie weisen darauf hin, dass sich die Mittelwerte der März-Temperaturen in Potsdam für 1917 und 2013 um 5/100 Grade unterscheiden.
Diese Information ist völlig sinnfrei, da der Verlauf der Tagesmittel in diesen beiden Monaten völlig unterschiedlich war.
Für das Pflanzenwachstum ist es z.B. sehr wichtig, ob die kälteren Tage zum Anfang oder zum Ende des Monat März aufgetreten sind.
Daher ist es sinnvoll, wenngleich auch noch ziemlich grob, die Mittelwerte aus den Tagesmitteln (in Potsdam) für die jeweils zweite Märzhälfte zu betrachten. Es ergeben sich für 1917: 0,8°C +/- 0,77°C(SEM) resp. für 2013: -1,5°C +/- 0,47°C(SEM). Diese sind signifikant(Mann-Whitney test) verschieden – im Gegesatz zu den Monatsmitteln der beiden Jahre.
[Antwort: Es freut uns, wenn unsere Beiträge zu weiteren Analysen anregen. Aber verraten Sie unseren Lesern, wie Sie auf einen Unsicherheit von 0,77 Grad in der Bestimmung der mittleren Temperatur für eine Monatshälfte kommen?
Ich habe nochmals nachgefragt, die Thermometer werden auf ein Zehntel Grad abgelesen. Nehmen wir an, der Ableser kann sich dabei um ein Zehntel nach oben oder unten vertun, dann ist die zufällige Unsicherheit der Einzelmessung +/- 0,1 Grad. Der Monatsmittelwert besteht aus 93 Einzelmessungen (3 mal täglich wird abgelesen), sodass die Unsicherheit in diesem Mittelwert um den Faktor Wurzel aus 93 reduziert ist. Daher beträgt die Unsicherheit im Monatsmittel nur ca. +/- 0,01 Grad. Nun kann es neben diesem Ablesefehler noch einen systematischen Fehler geben, etwa weil das Thermometer im Jahr 1917 anders geeicht war als im Jahr 2013. Aber gerade die Potsdamer Säkularstation ist ja berühmt dafür, dass hier lückenlos von 1893 bis heute mit den gleichen Instrumenten und gleichen Verfahren gemessen wurde, und auch 1917 konnte man ein Thermometer schon präzise eichen. Letztlich ist es auch unwichtig, ob der März 1917 nun einen Hauch kälter war als 2013 oder umgekehrt, sagen wir einfach sie waren nahezu gleich kalt. Mein Hauptargument ist ja, dass der März 2013 in einem deutlich wärmeren Klima stattfand und daher umso ungewöhnlicher ist – und hier reden wir von einem um ca. 1 Grad wärmeren Klima (auf den genauen Wert kommt es hier auch nicht an), was auf jeden Fall ein Vielfaches der Messungenauigkeiten beträgt. Stefan Rahmstorf]
@ Dr. Schulze
ihr Wissen über den Einfluss von Temperaturabweichungen im März auf das Pflanzenwachstum in Allen Ehren, aber was hat das mit der globalen Erwärmung zu tun, die allem Anschein nach immer mehr zu einem Problem wird?
Wenn Sie es in ein oder 2 leicht verständlichen Sätzen erklären könnten, wäre nett 🙂
Beginn der Zeitreihe in Kleiner Eiszeit
Sehr geehrter Prf. Rahmstorf,
ausgehend von der sog. Kleinen Eiszeit (mit niedriger Sonnenaktivität) wundert es nicht, dass die Märztemperaturen einen steigenden Trend anzeigen. Zudem fehlt zur Trendlinie der Vertrauensbereich, also das Konfidenzintervall. Auch ergibt sich in den letzten 20 Jahren kein beschleunigter Anstieg, sondern ein entschleunigter.
MfG
Martin Schindler
[Antwort:Lieber Herr Schindler – die Ursache der globalen Erwärmung ist nicht Thema dieses Beitrags – schauen Sie dazu z.B. hier. Das Konfidenzinterval des oben gezeigten Trends ist 0.7 +- 0.5 Grad pro Jahrhundert; Sie sehen daran bereits, dass angesichts des starken “Rauschens” eine Aussage über den Trend nur der letzten 20 Jahre sinnlos ist. Stefan Rahmstorf]
Grafik mit Konfidenzintervall
Sehr geehrter Prof. Rahmstorf,
hier einmal Ihre Grafik mit 95 %-Konfidenzintervall (Vertrauensbereich).
http://tinyurl.com/dys866p
Die Trends – sowohl der langfristige, als auch der über die letzten 20 Jahre – bewegen sich natürlich innerhalb der Unsicherheiten, so dass sie nicht aussagekräftig sind.
MfG
Martin Schindler
Der Frühling
Sehr geehrter Herr Rahmstorf,
ich habe immer noch nicht verstanden, wieso zum einen die kalten Temperaturen um diese Jahreszeit eine Folge der Eisschmelze sein sollen, wir also folglich in Zukunft mit sehr kalten Frühlingen häufiger zu rechnen haben, Ihre Seite http://www.klimafolgenonline.com aber für den Frühling in den nächsten Jahrzehnten stets eine stärkere Erwärmung in den meisten Regionen Deutschlands vorhersagt als für Sommer und Herbst. Sehen Sie hier keinen Widerspruch?
[Antwort: Diese Grundfrage kommt in den Kommentaren in immer neuen Varianten. Wie ich schon mehrfach betont habe: wenn die zitierten Studien stimmen und häufiger mit Kaltlufteinbruch zu rechnen ist, bedeutet das noch lange nicht, dass insgesamt die Winter oder Frühlinge in Deutschland kälter werden. Das war ja auch in den letzten Jahren nicht so. Beispiel der Winter 2011/12: da hatten wir einen extremen Kaltlufteinbruch im Februar, bei dem in Europa Kälterekorde in langjährigen Zeitreihen gebrochen wurden, aber insgesamt war der Winter nicht besonders kalt. Stefan Rahmstorf]
na und?
sieht man sich die sg “Ausreißer” an, zeigt sich ganz einfach, dass diese Monatsmittel der T da und dort eben stark varieren. In etwa genau so stark wie eh und je. Nur weil gerade dieses jahr ein kaum zu unterscheidende Max. zu gewissen anderen Jahren aufgetreten ist, sollte man daraus gar nix implezieren. Das ist der Lauf der Dinge, ganz einfach. Würde man auch bei anderen Monaten da und dort immer wieder finden.
Die fragwürdigste Studie, hier von Rahmstorf verlinkt, ist nichts weiter als eine sehr fragwürdige Erlärung für diverse GWL Häufigkeiten in Großraum N Eurasien/ Europa. Die Teile der Kara See sind flächenmäßig im Promille Bereich der NHK angesiedelt und wegen nochmals im Prozent Bereich davon wegen Eisflächen usw. daraus “kältere” Winter irgendwo in Europa zu konstruiren, ist nichts weiter als ein Versuch. Ein Versuch von Leuten, die es nicht wahr haben wollen, dass Klima eben nicht nur CO2 ist. Traurig, aber real.
@ Rahmstorf, @ RD
+/-SEM ist +/- Standardabweichung/Quadratwurzel(n), oder wenn Sie es nicht gegenwärtig haben sollten: der mittlere Fehler des Mittelwertes mit einem Konfidenzintervall von 67%.
n ist die Anzahl der zur Mittelwertbildung benutzeten Tagesmittel, deren Verteilung für die zweite Märzhälfte 2013 gerade noch die Kriterien einer Gaussverteilung erfüllt. Konservativ habe ich deswegen die Verschiedenheit zum Vergleichsintervall von 1917 mit einem nichtparametrischen Test abgeschätzt.
Warum sollte ich mich zu globaler Erwärmung äüßern, wenn ich einen Artikel “analysiere”, der von den Temperaturen der Säkularstation Potsdam handelt?
Mit freundlichen Grüßen
E.Schulze
[Antwort: Lieber Herr Schulze, ich vermute, Sie haben hier einen Denkfehler gemacht, und die Streuung der einzelnen Messwerte wie einen zufälligen Messfehler behandelt (siehe meine Antwort auf Ihren ersten Kommentar). Bei dieser Streuung handelt es sich aber um ganz reale Temperaturveränderungen, nicht um Messunsicherheiten, die eine entsprechende Unsicherheit im Monatsmittelwert mit sich bringen würden. Stefan Rahmstorf]
Grönland
Bemerkenswert ist auch die Tatsache, dass die westgrönländische Küste von Ende März bis gestern teils zweistellige Plusgrade verzeichnen konnte und überall Rekorde gebrochen wurden. Siehe hier: http://www.wunderground.com/…4/DailyHistory.html
Und nicht nur an diesem einen Punkt sondern auf der ganzen Westküste.
Vielen Leute ist nicht der energieerhaltende Charakter der Großwetterlagen bewusst – bei uns ist es ja nicht kalt, weil Energie fehlt oder “vernichtet” wurde, sondern weil die warme Atlantikluft, die uns sonst wärmt, stattdessen nach Nordwesten gequetscht wurde und jetzt Grönland und Labrador zum Schmelzen bringt.
Wenn es irgendwo mal ein paar Tage kalt ist, muss es zwangsweise woanders im gleichen Maße wärmer sein – manchmal kann man dieses “woanders” wie jetzt gerade gut sehen, manchmal versteckt es sich im Rest der Atmoshphäre oder in den Ozeanen. Aber es ist da.
Klimawandel findet auf der Meta-Ebene darüber statt. Das Wetter ist eine Fußballmannschaft, die auf dem Rasen trainiert und Klima ist der Trainer an der Seite, der weitere Bälle reinwirft. Vielleicht sollte man das in der öffentlichen Diskussion stärker betonen.
Diskussion zum Thema
Am Sonntag abend befaßte sich eine Diskussionssendung im ORF mit dem Thema.
Abstruse Ansichten eines Mathematikers und eines Leiters einer “Denkfabrik” .. unglaublich eigentlich.
Dann kam wieder die Vorhalte: Ja, der Herr Latif hat im Jahr 2000 behauptet, daß keine schneereichen ….
Frau Kromp-Kolb hat ihn verteidigt; fand ich gut !
Nachfrage
Ich verstehe Ihre Antwort so: Obwohl wir statistisch häufiger mit Kälteeinbrüchen aufgrund der arktischen Eisschmelze zu rechnen haben, stehen Sie zu den Prognosen von KlimafolgenOnline, wonach es in den nächsten Jahrzehnten gerade im Winter und Frühling in Deutschland wärmer wird.
Demnach muss es also einen Effekt geben, der die häufigeren Kälteeinbrüche überkompensiert, denn wie schon mehrfach geschrieben wird von Ihrem Institut ja eine stärkere Erwärmung für Winter und Frühling als für Sommer und Herbst prognostiziert. Um welchen Effekt handelt es sich hierbei?
[Antwort: Um den Treibhauseffekt aufgrund der steigenden Treibhausgaskonzentrationen. Stefan Rahmstorf]
Mess- und Denkfehler
Sehr geehrter Herr Prof. Rahmsdorf,
meine “Analyse” – wie Sie es nennen – bezieht sich nicht auf Messfehler. Die Frage danach hat Herr Walton gestellt.
Sie haben die Zeitreihe der jährlichen arithmetischen März-Mittelwerte der mittleren Tagestemperaturen der Säkularstation Potsdam Telegrafenberg dargestellt. Diese Art der Mittelwertbildung setzt bekanntlich voraus, dass die Tagestemperaturen innerhalb des Monats (auf definierten Konfidenzniveau) normalverteilt sind. Nur wenn Sie dieses Kriterium zutrifft, ist die Berechnung einer Regressionsgeraden auf Basis der Monatsmittel zulässig. In diesem Fall könnten Sie auch mithilfe eines geeigneten Tests entscheiden, ob sich deren Steigung signifikant von Null unterscheidet.
Zwar geben Sie ein Konfidenzintervall von 0,2 bis 1,2 pro 100 Jahre für die Gerade an, teilen jedoch nicht das Konfidenzniveau mit.
Diese Angabe ist wissenschaftlicher Standard: sie ist Voraussetzung um signifikante Unterschiede abzusichern und zu qualifizieren. In den Disziplinen, in denen Inferenzstatistik zum unabdingbaren Repertoire gehört, wird ein Konfidenzniveau von mindesten 95% gefordert. Bezogen auf obige Daten ergibt sich ein Intervall von -0,18 bis 1,58 pro 100 Jahre für das Konfidenzniveau von 95%, auf welchem sich die Steigung der von Ihnen berechneten Regressionsgeraden nicht signifikant von null unterscheidet.
All diese Aussagen sind nur dann sinnvoll (und mathematisch zulässig) wenn, wie schon betont, die Tagesmittel innerhalb des Monats normalverteilt sind. Aber aus welchem Grunde sollten sie das sein?
Die Tagestemperaturen werden von vielerlei Einflussgrößen bestimmt, die in ihrer Komplexität und Unüberschaubarkeit zu Werten führen, die an Zufallsereignisse erinnern und daher auch oft als solche behandelt werden (auch ich habe in meiner ersten Zuschrift die Monatsmittel als arithmetisches Mittel betrachtet und entsprechend einen SEM-Wert mitgeteilt). Formal richtig – da die Tagesmittel von März 1917 und 2013 die einschlägigen Normalitätstest erfüllen. Nicht so die Halbmonatsstichproben, weswegen ich auf einen nichtparametrischen Test zurückgegriffen habe, um diese zu vergleichen.
Die Analyse von Temperaturzeitreihen sollte daher meiner Meinung nach mit parameterfreien Methoden erfolgen: Mittelwerte durch Mediane und Streuungen durch Perzentile charakterisiert werden.
Dies würde zumindest die Gläubigkeit an Regressionsgeraden vermeiden, da sich diese für nichtparametrischen Größen gar nicht erst berechnen lassen.
Dies führt zu einer weiteren grundsätzlichen Frage. Warum sollten Temperaturzeitreihen linearen Trends unterliegen und wodurch wird die zutreffende Intervallgröße der Trendanalyse bestimmt?
Sie implizieren in Ihren Anmerkungen einfach: Je länger das Intervall, desto zutreffender die Trendberechnung. Das setzt aber einen linearen Verlauf der Temperaturänderungen voraus, was durch retrospektive Beobachtungen nicht belegt werden kann.
Mit besten Grüßen
E. Schulze
[Antwort: Lieber Herr Schulze, ich kann Ihrer Argumentation nicht folgen. Selbstverständlich kann ich einen Mittelwert über Messungen berechnen, die nicht normalverteilt sind. Nehmen wir als Beispiel an, in der ersten Märzhälfte sei es dauernd konstant 0 Grad gewesen, und in der zweiten dauernd 10 Grad. Dann ist der Mittelwert über den ganzen März 5 Grad, obwohl die Temperaturen alles andere als normalverteilt waren. Und wenn jede Einzelmessung eine zufällige Messungenauigkeit von +/- 0,1 Grad hat, dann ist die Genauigkeit des Mittelwerts viel größer, um den Faktor 1 durch die Wurzel der Anzahl der Messungen. Wie Sie zu der These kommen, die Ungenauigkeit in einem Mittelwert könne 0,5 Grad betragen, obwohl die Einzelmessungen viel genauer sind, haben Sie nicht erklärt. Ich kann nur vermuten, Sie behandeln die einzelnen Messwerte wie Versuche, eine konstante Größe zu messen – etwa so, wie wenn Sie hundert Messungen der Gravitationskonstanten machen, und die einzelnen Messungen streuen und liefern so hundert ungenaue Schätzwerte – nicht weil die Graviationskonstante sich geändert hätte, sondern aufgrund von Messfehlern. Dann ergeben Ihre Ausführungen einen Sinn. Dieser Fall liegt hier aber nicht vor – die Messwerte der Temperatur streuen von Tag zu Tag und Stunde zu Stunde, weil sich eben tatsächlich die Temperatur ändert.
Eine weitere mögliche Frage wäre, inwieweit die drei täglichen Messungen eine gute Abschätzung des Tagesmittelwertes liefern, den Sie erhalten würden, wenn Sie etwa jede Minute messen würden. Eine interessante Detailfrage, die allerdings irrelevant wird, wenn Sie den Begriff “Monatsmittelwert” für den Zweck des Vergleiches einfach nur als Mittelwert über alle Messungen in dem jeweiligen Monat verstehen. Mehr soll die obige Grafik nicht darstellen, sie zeigt einfach den so definierten Mittelwert. Relevant ist ja vor allem die Vergleichbarkeit mit allen Vorjahren, die hier gegeben ist. Stefan Rahmstorf]
Im Interview: Text
Mojib Latif zum kalten Frühling 2013:
http://science.orf.at/stories/1715841/
Mittelwerte fallen nicht vom Himmel
Sehr geehrter Herr Prof. Rahmstorf,
BITTE VERWENDEN SIE NUR DIESEN KOMMENTAR!
IN DER KURZ VORHER ABGESANDTEN VERSION HATTE ICH EIN FALSCHES ERBENIS MITGETEILT. Danke
wie Sie richtig anmerken: “die Messwerte der Temperatur streuen von Tag zu Tag und Stunde zu Stunde, weil sich eben tatsächlich die Temperatur ändert”
Beschränken wir uns vorerst auf die Tagesmittel, so kann Ihre Verteilung z. B. bezogen auf einen Monat dargestellt und ein Verteilungstyp charaktirisiet werden.
Weiterhin schreiben Sie u. a.: “…wenn Sie den Begriff “Monatsmittelwert” für den Zweck des Vergleiches einfach nur als Mittelwert über alle Messungen in dem jeweiligen Monat verstehen. Mehr soll die obige Grafik nicht darstellen, sie zeigt einfach den so definierten Mittelwert. Relevant ist ja vor allem die Vergleichbarkeit mit allen Vorjahren, die hier gegeben ist.”
Mit dieser Vereinfachung kann ich mich als Wissenschaftler nicht zufriedengeben. Wenn ich über die Information verfüge, aus welchen Einzelwerten ein Mittelwert entstanden ist, muss ich, um Mittelwerte aus unterschiedlichen Grundgesamtheiten bewerten zu können, Informationen über die Verteilung mit einbeziehen.
Vergleichen aber kann ich nur Mittelwerte, die aus gleichen, oder (im Rahmen zu definierender Konfidenzen) ähnlichen Verteilungstypen entstanden sind.
Unter den März-Monatsmitteln der Potsdamer Temperaturreihe finden sich 6 arithmetische Monatsmittel zwischen 4,9°C und 5,1°C, die aus unterschiedlichen Verteilungen der Tagesmittel basieren. (Nur drei von diesen erfüllen einen Normalverteilungs-Test auf einem 95% Konfidenzniveau.)
Dies äußert sich auch in den Medianen, die eine Spanne von 4,6°C bis 5,8°C überdecken.
Nur wenn alle 6 Monatsmittel auf dem gleichen Verteilungstyp der Tageswerte basierten, stimmten arithmetische Mittel und Mediane überein. Bei unterschiedlichen oder ungeklärten Verteilungstypen ist der Median geeigneter zur Darstellung eines Mittelwerts.
Also sollte es doch selbstverständlich sein, eine Information über die Verteilung in die Darstellung von Mittelwerten einzubeziehen.
Warum werden solche Differenzierungen in der Klimatologie mißachtet?
In Disziplinen wie z. B. Biologie, Medizin oder Landwirtschaft sind die Anwendung deskriptiver und induktiver Statistik unabdingbar, insbesondere für Veröffentlichungen und Abschlussarbeiten.
Zu der von Ihnen angeregten Frage der geeigneten Messintervall bei der Ermittlung von Tagesmitteltemperaturen empfehle ich Ihnen:
“Beschreibung der Datenbasis des NKDZ von Johannes Behrendt et al.; 2011”
http://tinyurl.com/cqmjlfs
Abschließend lege ich ihnen ein “statistisches Gedicht” von H. P. List ans Herz:
Ein Mensch, der von Statistik hört,
denkt dabei gleich an MITTELWERT.
Ein Jäger auf der Entenjagd
hat einen ersten Schuss gewagt.
Der Schuss, zu hastig aus dem Rohr,
lag eine gute Handbreit vor.
Der zweite Schuss, mit lautem Krach,
lag eine gute Handbreit nach.
Der Jäger spricht ganz unbeschwert
voll Glauben an den MITTELWERT:
Statistisch ist die Ente tot!
Doch wär´er klug und nähme Schrot,
dies sei gesagt, ihn zu bekehren,
er würde seine Chancen mehren:
Der Schuss geht ab, die Ente stürzt,
weil STREUUNG ihr das Leben kürzt.
In diesem Sinne
E. Schulze
[Antwort: Hier müssen wir wohl “agree to disagree”, wie es so schön heißt. Das Beispiel mit der Ente ist ja wieder eines, wo es einen “richtigen” Schuss gibt (den Treffer – wie bei dem Beispiel der Gravitationskonstanten den richtigen Wert). Die einzelnen Temperaturmessungen sind aber nicht Versuche, den “richtigen” Wert zu Treffen (also das Monatsmittel), sondern einfach nur Messungen der zu diesem Zeitpunkt herrschenden Temperatur, nicht mehr und nicht weniger. Den Mittelwert aus diesen Messungen zu bilden ist informativ – ganz unabhängig von Annahmen oder Erkenntnissen über die Verteilung der Messwerte (die mich natürlich zusätzlich interessieren könnte). Ich kann zum Beispiel den Jahresmittelwert interessant finden, obwohl die Messwerte im Jahr aufgrund des zugrunde liegenden etwa sinusförmigen Jahreszyklus alles andere als Normalverteilt sind. Stefan Rahmstorf]
März global
Der März 2013 war global gemittelt der 9.- wärmste seit Beginn der Aufzeichnungen (Giss):
http://data.giss.nasa.gov/…ta_v3/GLB.Ts+dSST.txt
Man sieht deutlich, dass es sich beim kalten März in Mitteleuropa und Teilen Sibiriens um regionale Kälte handelte und nicht um ein globales Phänomen!
http://data.giss.nasa.gov/…dius=1200&pol=reg
Azustralien erlebte die heisesten Monate Dez 2012-Feb.2013 seit Beginn der Aufzeichnungen:
http://www.dwd.de/…1302_tmperatur_australien.pdf
Die durchschnittlichen Oberflächentemperaturen der gesamten Erde für den Monat Februar 2013 haben deutlich gezeigt, dass es in vielen Ländern der Welt, vor allem aber in Russland, Kanada, Australien und Alaska, bis zu fünf Grad Celsius wärmer gewesen ist als normal. Eine Ausnahme haben lediglich die Region Kalifornien und Mitteleuropa gebildet.
Das straft all diejenigen Lügen, die meinten, mit dem kalten März in Mitteleuropa den globalen Klimawandel widerlegen zu können….
2000 Jahre Klimadaten
Sehr geehrte KlimaLounge-Blogger,
heute habe ich einen Bericht bei SpiegelOnline entdeckt, der über eine Arbeit berichtet, in der in mühsamer Kleinarbeit aus hunderten verschiedener Klimaarchive der Temperaturverlauf für 2000 Jahre herausgearbeitet wurde.
(“http://www.spiegel.de/wissenschaft/natur/temperatur-daten-klima-der-vergangenen-2000-jahre-fuer-alle-kontinente-a-895356.html”)
Meiner Meinung nach faszinierend.
Leider waren sich die Kommentare fast alle dahingehend einig, dass dieser Bericht “beweise” , dass Klimaabkühlung Hochkulturen vernichte und somit die bisherige Erwärmung doch gut sei und fortgesetzt werden solle.
Deswegen möchte ich sie bitten, sich diese Studie anzusehen und darüber einen Post zu verfassen, wenn sie Zeit haben.
mit freundlichen Grüßen
SciLog-Fan
[Antwort: Ist geplant – kann aber noch etwas dauern, leider ist nicht immer Zeit zum Bloggen! Danke für das Interesse. Stefan Rahmstorf]
Bleyfuß
@Achim Linke
SpOn-Redakteur Axel B. enttäuscht mal wieder nicht.. und bedient die Klientel, die entweder bunt unterhalten werden will oder die den KW als “Laune der Natur” einstufen möchte.
Zu 2000 Jahre Klimadaten …
… besser hier schauen:
http://www.scinexx.de/…ell-15980-2013-04-22.html
Wie zu erwarten, vermeinen diverse Klimaerwärmungsskeptiker daraus ableiten zu können, daß das CO2-forcing eh nicht so schlimm sei.
Streuungsmaße
Betreffs der Diskussion mit Herr Schulze über das Konfidenzintervall der Monatshälften: Herr Schulze hat das m.E. korrekt gemacht. Streuungsmaße haben im Normalfall ja gar nichts mit Messungenauigkeiten zu tun, wie Herr Rahmsdorf anscheinend annimmt (höchstwahrscheinlich habe ich ihn missverstanden?), sondern beziehen sich eigentlich immer auf ganz reale, “echte” Werte (Körpergrößen von Personen, Korngewichte) und beschreiben die Stärke der realen Streuunng innerhalb der Stichprobe (hier halt je 93 Temperaturmessungen). Ich wüsste nicht, dass ich in diversen Statistikkursen jemals ein Beispiel gehabt hätte, wo es nicht um real vorhandene Unterschiede ging.
Wenn man jetzt meinetwegen alle angegebenen Märzmitteltemperaturen in Potsdam (oder wie Herr Schulze die Temps einer einzelnen Märzhälfte ) als Messreihe nimmt und dafür den Standardfehler des Mittels (SEM) berechnet, so ist dies absolut sinnvoll, denn dieser Standardfehler kann uns sagen, wie viel ein Mittelwert Potsdamer Märzmitteltemperaturen aus einer Zeitreihe eines anderen Jahres/Jahrhunderts abweichen dürfte, damit man davon ausgehen kann, dass die Märze des anderen Jahrhunderts/die andere Messung einer zweiten Märzhälfte noch zur selben Population gehört, d.h. sich die Märztemperatur in Potsdam nicht signifikant geändert hat. (Dafür muss, grob vereinfacht, der zweite Mittelwert im 95%-Konfidenzintervall des ersten liegen). Das ist die (parametrische) Standardmethode, einen signifikanten Unterschied zwischen zwei Stichproben, hier: Messreihen, festzustellen. In den t-Test geht der Standardfehler des Mittels als maßgebliche Größe ein. (Die Feinheiten der nichtparametrischen Verteilung ignoriere ich hier mal.) Also, Soweit ich sehe, sind Streuungsmaße auch bei klimawissenschaftlichen Temperaturmessreihen von Relevanz oder sollten es sein, da statistische Signifikanztests wesentlich auf ihnen basieren. Mit Ablesefehlern von Meteorologen hat das rein gar nichts zu tun. Aber ich denke wie gesagt auch, dass ich Herrn Rahmstorf missverstanden habe, denn so kann es eigentlich nicht gemeint gewesen sein. All the best, R. Berger
[Antwort: Liebe/r R. Berger, ich denke Sie haben mich doch richtig verstanden. Der entscheidende Punkt ist, dass das Streuungsmaß in diesem Falle einfach angibt, wie stark die einzelnen Märzmesswerte um den Mittelwert herum streuen. Das liegt z.B. am Tagesgang (nachts ist es meist kälter) und an den Wetterschwankungen von Tag zu Tag. Es hat aber nichts damit zu tun, wie genau ich den Mittelwert für einen einzelnen März (etwa den März 2013) bestimmen kann. Daher hat es auch nichts damit zu tun, wie sicher ich sein kann, dass der März 2013 wärmer oder kälter war als z.B. der März 1917. Es ging bei dieser Frage übrigens auch nicht darum, mit welcher Wahrscheinlichkeit der März 2013 eine Stichprobe aus derselben Population wie der März 1917 ist. (Wir wollen ja nicht durch Vergleich dieser Werte einen signifikanten Klimawandel nachweisen – das wäre abwegig und würde sicher nichts Signifikantes ergeben, dazu braucht man viel mehr Daten.) Es ging hier lediglich um den konkreten Einzelfall – mit welcher Genauigkeit kann ich den Mittelwert für einen einzelnen März feststellen und daher eine Aussage darüber treffen, ob er wärmer oder kälter als ein bestimmter anderer, einzelner März war. Stefan Rahmstorf]
Nochmal der Standardfehler…
Lieber Herr Rahmstorf, ganz vielen Dank für die fixe, nette Antwort (und die Arbeit die Sie in diesen Blog investieren).
“Daher hat es auch nichts damit zu tun, wie sicher ich sein kann, dass der März 2013 wärmer oder kälter war als z.B. der März 1917.”
In der rein deskriptiven Statistik (die Sie uns oben im Beitrag gegeben haben) nicht. In der Inferenzstatistik schon, und die ist bei Vergleichen nicht die unüblichste Methode. Der SEM sagt Ihnen natürlich nicht, wie genau Sie den Mittelwert für den einzelnen März bestimmt haben (den haben Sie sehr genau bestimmt!), sondern wie charakteristisch dieser Mittelwert wahrscheinlich für einen anderen März aus derselben Klimaperiode sein wird.
Ich gebe Ihnen recht, dass man der Meinung kann, beim Vergleichen von zwei Einzelmonaten seien Angaben zur statistischen Signifikanz und inferenzstatistische Methoden nicht sehr aussagekräftig und man könne darauf auch verzichten. Man kann sich sicher auch streiten, ob man, wenn man das trotzdem macht, nicht besser Tagesmittel eingehen lässt als alle Einzelmessungen, d.h. eine Glättung des Tag-Nacht-Laufs vornimmt, bevor man den Standardfehler berechnet. Die Signifikanz sagt uns allerdings hier schon, dass die zweite Märzhälfte 2013 ein echter Ausreißer war, auch im Vergleich mit 1917; Herrn Schulzes Rechnung ist also nicht sinnlos.
Was mir wichtig war zu sagen (sind wir uns denn da jetzt einig?): Ein Standardfehler hat in 99 % aller Anwendungen nicht in erster Linie mit Ablesefehler/Messfehler zu tun, sondern mit echter Variabilität in den Einzelwerten, egal, woher genau die Variabilität sich speist. Wenn Sie in einer Studie bei 100 Leuten immer wieder den Blutdruck messen, haben Sie intrapersonale Variabilität im Tagesgang genauso drin wie die interpersonale Varianz und eventuelle Messfehler. Statistische Methoden sind von Leuten aus den Lebenswissenschaften erarbeitet worden, wo es echte natürliche Abweichungen gibt, wie beim Wetter eben auch.
Können wir uns auch darauf einigen: Wenn man einen Klimawandel nachweisen will, wird man mit ganzen Jahrhunderten oder mit 30-Jahresabschnitten arbeiten. Aber eine dafür geeignete Methode ist eben genau diese (t-Test zweier Meßreihen, in den der SEM eingeht). Signifikanzen berechnen sich immer auf Basis der Varianz in Bezug auf die Anzahl der Messungen, weil die einem einen Eindruck geben, ob Abweichungen unterschiedlicher Mittelwerte eher auf Zufall oder eher auf systematischen Unterschieden beruhen.
Sie persönlich arbeiten sicher mehr mit linearen Korrelationen in der Zeit als mit Mittelwertvergleichen, aber dann kriegen Sie ja auch ein Konfidenzintervall für beta und eine Signifikanzangabe, und das beruht letztlich auf der gleichen Basis, wenn es auch etwas komplizierter zu berechnen ist. Und “Error” bei der Korrelation ist auch nicht Messfehler, sondern das ist der Teil der real vorhandenen Varianz, der sich nicht durch den Korrelationskoeffizienten erklären lässt.
Beste Grüße, Ruth Berger
“Error” bei der Korrelation…
im letzten Satz hätte ich natürlich statt Korrelation Regression schreiben wollen!
Herzl. Gruß, R. Berger
2000 Jahre Klimadaten
Das Pages 2k- Projekt ist sicher herausragend, keine Frage. Nur macht es die Klimawissenschaft wohl nicht einfacher.
Das nicht zeitsynchrone Auftreten bestimmter Klimasignale, die aber wohl gemeinsamen Ursprungs sind, stellt wohl neue Herausforderungen.
Eine davon könnte sein, in Zukunft das *Konzept des Globalklimas* vielleicht gar fallenzulassen auf kleineren und mittleren Zeitskalen und zu regionaleren Klimamodellen zu kommen.
Nur: Ob REMO das überlebt?
Allerdings könnte daraus ein besseres Verstehen von regionalen Abkühlungstrends resultieren und z. B. den gegenwärtigen wohl doch vorhandenen Erklärungsbedarf bezüglich kälterer Winter in Europa, speziell D., liefern.
Ich wäre sehr dafür, kann mir allerdings nicht vorstellen, wie das ohne Abstriche an der Rolle des Co2 abgehen wird. Hier wird es dann wohl ein Problem geben.
@ H. Müller
Ich bin der Meinung, daß für konsistentes Daten sammeln und Regionalklimaanalysen die “ZAMGs” – wenn ich das mal so nennen darf – der jeweiligen Länder zuständig sind/wären.
Wenn ich das richtig sehe, greift “2000 Jahre Klimadaten” doch auf solche Daten zurück und bereiteten sie dementsprechend auf.
Institute wie PIK und Geomar betrachten die Klimaentwicklung global.
Ich finde, man sollte das Streben nach immer kleineren Regional-Klimaeinheiten nicht übertreiben.
Wie war das Klima meines Alpenheimattales der Größe 10x10km über die letzten 5000 Jahre ? Wäre natürlich hochinteressant.
Warum die Einschätzung der Klimawirksamkeit von CO2 aufgrund “2000 Jahre Klimadaten” “korrigiert” werden sollte, will sich mir nicht erschließen.
Lied singen..
Erwärmung so real wie die Grünen in der Mitte. Ich kann jedenfalls ein Lied von singen:
http://schlichtgutemusik.de/#55f/custom_plain
Grüße und Dank an SciLogs&Klimalounge.
Ihr Olli Rack
400 ppm Carbon Dioxide surpassed !
http://researchmatters.noaa.gov/…ches400ppm.aspx
http://co2now.org/
Das Anstiegstempo ist ja Wahnsinn.
Das Ungleichgewicht zwischen anthropogenem Forcing und derzeitiger Meeresspiegelhöhe wird immer größer.
Es ist mit sprunghaften MSPL-Anstiegsschüben zu rechnen. Ich sehe das wie bei der Plattentektonik: Der Druck in den Gesteinsmassen steigt und steigt und irgendwann kommt es zu Ausgleichsvorgängen, sprich Erdbeben.