Einstein verstehen VI: Was heißt es, das Bezugssystem zu wechseln?
BLOG: RELATIV EINFACH

Dies ist Teil VI einer Online-Einführung in die Spezielle Relativitätstheorie, die hier im Blog einen “Testlauf” absolviert und später – u.a. durch Feedback der Blogleser verbessert – ein Teil des Webportals Einstein Online werden soll. Nähere Informationen zu den Hintergründen finden sich in Einstein verstehen: Ein Blogexperiment, Teil I.
[Derzeit sind online: Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7]
Noch geht es in der Einleitung um die “Vorarbeiten”: um diejenigen Konzepte aus der klassischen Physik – der Physik vor Relativitätstheorie und Quantentheorie – die man kennen muss, um zu verstehen, vor welchem Hintergrund und auf welcher Grundlage Einstein die Spezielle Relativitätstheorie einführte.
In den vorangehenden Teilen IV und V habe ich die Gesetze der klassischen Mechanik vorgestellt. Dass es mindestens ein Bezugssystem gibt, in dem die Gesetze in der dort geschilderten einfachen Form gelten, war dabei zunächst eine Annahme gewesen. In diesem und den darauf folgenden Teilen beschäftigt uns die Frage, ob und wieweit sich die Form der physikalischen Gesetze ändert, wenn wir von dem in Teil IV und V gewählten zu einem anderen Bezugssystem übergehen.
Dass sich die Form der Gesetze bei bestimmten Übergängen nicht ändert, ist Ausdruck verschiedener Spielarten des Relativitätsprinzips, das wir in einem späteren Teil noch näher kennenlernen werden. Wie der Name bereits andeutet, wird dieses Prinzip später ein wichtiger Baustein der Speziellen Relativitätstheorie.
Dass sich die Form der Gesetze bei bestimmten anderen Übergängen doch ändert, wird uns später helfen, die in Teil IV und V genutzten Inertialsysteme zu definieren – die Systeme, in denen die Gesetze der klassischen Mechanik die in Teil IV und V vorgestellte einfache Form haben. Auch diese besonderen Bezugssysteme werden wichtig, wenn wir später die Spezielle Relativitätstheorie beschreiben.
Dazu, die verschiedene Spielarten des Relativitätsprinzips einzuführen, fehlen uns allerdings noch ein paar Grundlagen. Einen Teil davon liefert Teil VI hier, nämlich Informationen zur Vielfalt der Bezugssysteme und dazu, wie der Übergang von einem in ein anderes Bezugssystem überhaupt beschrieben werden kann. In Teil VII wird es dann um konkrete Beispiele gehen, und in Teil VIII kommt dann das Relativitätsprinzip: Dort wenden wir uns der Frage zu, welche Form die physikalischen Gesetze in den durch die in Teil VIII vorgestellten Übergänge erreichbaren Bezugssystemen haben.
Idealisierte Punkte im Raum
Ein Bezugssystem erlaubt es uns, Orte mit Hilfe von Raumkoordinaten zu beschreiben und Zeitpunkte mit Hilfe einer Zeitkoordinate. Wie man den Raum vermisst und jedem Ort ein Tripel x,y,z von kartesischen Koordinaten zuordnet, hatte ich in Teil I geschildert, die Grundlagen der Zeitmessung in Teil II und verschiedene Möglichkeiten, Gleichzeitigkeit zu definieren und auf dieser Grundlage den Zeitpunkt eines Ereignisses auf einer Referenzuhr abzulesen, in Teil III.
Wir haben dort auch gesehen, welche Festlegungen wir treffen müssen, um ein Bezugssystem zu definieren: Für die räumlichen Achsen müssen wir zunächst unseren Raumnullpunkt wählen und dann die drei Achsenrichtungen – wie das z.B. durch die Angabe von drei Punkten geht, deren Abstände voneinander sich freilich nicht ändern dürfen, hatte ich in Teil I hier vorgeführt.
Mit einer Referenzuhr, deren Zeitanzeige man mit Hilfe einer der in Teil III beschriebenen Gleichzeitigkeitsdefinitionen auch Ereignissen an allen anderen Orte im Raum zuweist, kommt eine Zeitkoordinate hinzu.
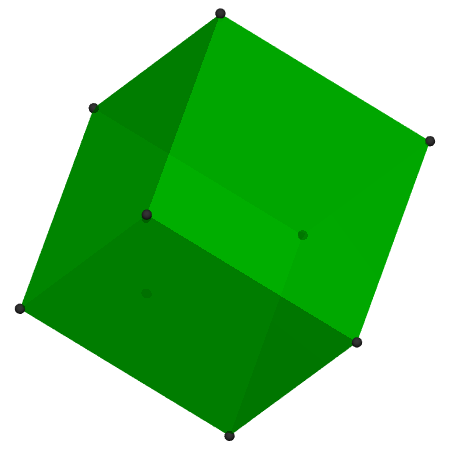 Von der wirklichen Welt und den räumlichen Eigenschaften ihrer Objekte zur Geometrie des euklidischen Raums waren wir über Idealisierungen gelangt: Sehr kleine Objekte, etwa winzigste Markierungen, haben wir in guter Näherung durch Punkte im euklidischen Raum modelliert.
Von der wirklichen Welt und den räumlichen Eigenschaften ihrer Objekte zur Geometrie des euklidischen Raums waren wir über Idealisierungen gelangt: Sehr kleine Objekte, etwa winzigste Markierungen, haben wir in guter Näherung durch Punkte im euklidischen Raum modelliert.
Viele dieser Punkte lassen sich indirekt definieren: Wenn wir beispielsweise einen näherungsweise würfelförmigen Körper wie in dem Bild rechts als Würfel im euklidischen Raum modellieren, dann sind hat dieser mathematische Würfel acht Eckpunkte – diese wiederum stehen in dem Modell für die Eckpunkte des wirklichen Würfels, selbst wenn jene evt. schon etwas abgestoßen oder allgemein etwas abgerundet sind.
In der klassischen Mechanik waren wir ähnlich vorgegangen und hatten zunächst in Teil IV als einfaches Modell Massepunkte oder Punktteilchen eingeführt, anschließend daraus dann in Teil V komplexere Modelle definiert, zuerst starre Körper und später die noch realistischeren elastischen oder sogar plastischen Körper.
(Und auch in solchen Abbildungen wie der oben rechts sind die Eckpunkte durch vergleichsweise kleine, aber eindeutig nicht punktförmige Kügelchen, oder durch kleine Flächen dargestellt, an denen gemalte Linien zusammenlaufen!)
Haben wir erst einmal begonnen, den uns umgebenden Raum und die darin befindlichen Objekte auf diese Weise zu modellieren, können wir Koordinaten einführen. Wir suchen dazu, wie in Teil I beschrieben, in der Wirklichkeit Entsprechungen zu jenen Größen, die man benötigt, um im euklidischen Raum ein (kartesisches) Koordinatensystem zu definieren – dem Raumnullpunkt und drei weiteren Punkten, deren Abstände untereinander konstant sein sollen, um die Achsenrichtungen festzulegen.
Dann können wir jedem Ort im Raum, dem wir einen geometrischen Punkt P zu geordnet haben, durch entsprechende Messungen Raumkoordinatenwerte x(P), y(P) und z(P) zuordnen.
Zeitpunkte
Kommen wir zur Zeit. Auch das, von dem wir im Alltag sagen, es würde in einem “Moment” oder “Augenblick” oder an einem “Zeitpunkt” stattfinden, ist jeweils ein Vorgang sehr kurzer, aber nicht unendlich kurzer Dauer: ein plötzlicher Knall, der Zusammenstoß zweier Kugeln, das Springen des Uhrzeigers in eine neue Stellung.
Mit den in Teil II vorgestellten Uhren können wir die Dauer solcher kurzen Vorgänge messen und zumindest in Gedanken den Übergang zur Idealisierung, zum unendlich kurzen Vorgang vornehmen. Unser Modell der immer weiter fortschreitenden Zeit ist die Zeitgerade, und jeder unendlich kurze Vorgang entspricht einem Punkt auf dieser Zeitgeraden: einem Zeitpunkt T.
In guter Näherung können wir auch sehr kurze Vorgänge beschreiben, indem wir ihnen auf der Zeitgerade einen einzigen Zeitpunkt zuordnen. Mithilfe unserer Referenzuhr und eines Gleichzeitigkeitsbegriffs können wir solchen Zeitpunkten wie in Teil III beschrieben eine Zeitkoordinate t(T) zuordnen: Den von unserer Referenzzeit angezeigten Zeitwert zum Zeitpunkt T.
Solche Zeitpunkte lassen sich dann wiederum als Elementarbausteine verwenden: Wir verwenden die Zeit als Parameter, um einen Vorgang zu beschreiben, etwa das Hin- und Herschwingen eines Pendels. Dazu schreiben wir messbare Größen wie die Auslenkung des Pendels φ als Funktion der Zeit, φ(t). Möglichst kurz andauernde Messungen der Auslenkung ordnen wir den entsprechenden Zeitpunkten auf unserer Zeitgerade zu und versuchen so, die Funktion φ(t) aus den Messwerten zu rekonstruieren oder einen angenommene Funktionalzusammenhang φ(t), also ein mathematisches Modell für die zeitliche Entwicklung der Pendelauslenkung, zu überprüfen.
Idealisierte Zeitpunkte in der Raumzeit
Als Kombination von Raum- und Zeitpunkt kann man noch eine weitere idealisierte Größe definieren, die in der Physik Punktereignis oder kurz Ereignis heißt. Ein Ereignis E ist dabei ein Geschehen, das an einem einzigen Raumpunkt P zu einem genau definierten Raumpunkt T stattfindet. Wir können symbolisch schreiben E=(P,T).
Mathematisch gesehen kann man dreidimensionalen Raum und Zeitgerade zu einem vierdimensionalen Gebilde zusammenfassen, das “Raumzeit” genannt wird. Darauf, was es mit dieser Kombination von Raum und Zeit zur Raumzeit im Einzelnen auf sich hat, werde ich später im Zusammenhang mit der Speziellen Relativitätstheorie noch genauer eingehen. Die Vierdimensionalität sagt nichts anderes aus, als dass man in jedem Bezugssystem vier Angaben benötigt, um ein bestimmtes Ereignis eindeutig zu definieren: die drei Werte der Ortskoordinaten und den Wert der Zeitkoordinate.
Damit sind Ereignisse so etwas wie Punkte in der (vierdimensionalen) Raumzeit. Im folgenden verwende ich die Begriffe “Raumzeitpunkt” und “Punktereignis” austauschbar.
Ebenso wie ein Raumpunkt und ein Zeitpunkt ist auch ein Punktereignis eine Idealisierung. In der wirklichen Welt gibt es zwar räumlich eng eingegrenzte, kurze Geschehnisse, bei denen Ort und Zeit in guter Näherung durch Angabe eines einzigen Raumpunkts und eines einzigen Zeitpunkts beschrieben werden. Solche tatsächlichen Ereignisse – eine räumlich eng begrenzte Explosion, oder das Zusammentreffen zweier sehr kleiner Objekte – sind selbst natürlich keine Punktereignisse. Aber wir nehmen sie, wie bei den Raumpunkten und Zeitpunkten auch, als Ausgang für unsere Idealisierung, derzufolge ein Punktereignis an einem einzelnen Raumpunkt stattfindet und von verschwindend geringer Dauer ist.
In Modellen der Welt, wie wir sie beispielsweise im Rahmen der klassischen Mechanik konstruiert haben, kommt den idealisierten Raum- und Zeitpunkten und damit auch den Punktereignissen eine wichtige Rolle zu. Wann immer dort beispielsweise ein Punktteilchen mit einem anderen Punktteilchen zusammentrifft, haben wir es mit einem eindeutig beschreibbaren Punktereignis zu tun.
Dass Physiker für “Punktereignis” oft kurz “Ereignis” sagen, kann zu Missverständnissen führen. Diese lassen sich aber recht einfach vermeiden, solange man sich darüber im klaren ist, dass das Wort Ereignis zum einen seine Alltagsbedeutung haben kann (etwas, das sich über einen begrenzten Zeitpunkt hin ereignet – die Schlacht von Waterloo, ein Autounfall, eine Sonnenfinsternis), zum anderen aber für Punktereignis stehen kann (findet an einem genau definierten Ort im Raum zu einem bestimmten Zeitpunkt statt). In der Regel ergibt sich aus dem Zusammenhang klar, welche der beiden Bedeutungen gemeint ist.
Was nicht vom Bezugssystem abhängt
Punktereignisse sind Modelle (oder Teile von Modellen) für physikalische Vorgänge, die sich in vielen Fällen auch ohne Rückgriff auf Koordinatenangaben beschreiben lassen. Gehen wir einen Schritt zurück: Wenn ein Teilchen A einsam durch den Raum fliegt, dann kann man diese Bahn beschreiben, wenn man Raumkoordinaten und eine Zeitkoordinate eingeführt hat. Aber ohne Rückgriff auf Koordinaten – oder äquivalente Messungen der Entfernung zu äußeren Bezugsobjekten – gibt es keine Unterscheidungsmerkmale, anhand derer sich ein Punkt der Bahn von den anderen unterscheiden ließe.
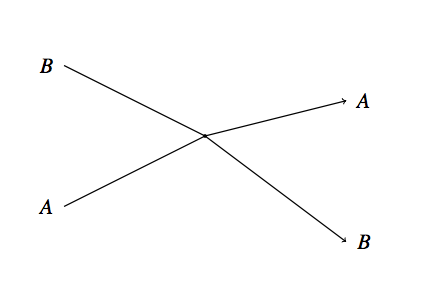
Ganz anders ist die Situation, wenn das Teilchen A an einer Stelle mit dem Teilchen B zusammenstößt und daraufhin beide Teilchen zurückprallen, wie hier skizziert:
“Der Ort und der Zeitpunkt, an dem Teilchen A mit Teilchen B zusammenstößt” ist, sofern Teilchen A und Teilchen B eindeutig identifizierbar sind, auch ohne jeglichen Bezug auf Koordinatenwerte eine eindeutige Beschreibung eines Punktereignisses E. Diese Beschreibung hängt nicht vom gewählten Bezugssystem ab: Die Aussage, dass Teilchen A und B zu einem bestimmten Zeitpunkt, an einem bestimmten Ort zusammentreffen, lässt sich ohne Rückgriff auf ein Bezugssystem vornehmen.
Ein solches Zusammentreffen – zwei verschiedene Objekte in guter Näherung an ein und demselben Ort, zur gleichen Zeit – wird auch als Koinzidenz bezeichnet. Koinzidenzen bilden so etwas wie eine elementare Struktur der physikalischen Geschichte – was trifft was, und in welcher Reihenfolge?
Betrachten wir eine solche Geschichte mit lauter Teilchen, die gegenseitig Zusammenstoßen und voneinander Abprallen, dann machen die Koinzidenzen freilich nur einen kleinen Teil dessen aus, was passiert. Zwischen den Zusammenstößen fliegen die Teilchen durch den Raum, auf dem Weg zum jeweils nächsten Rendezvous. Um diese Bewegung zu beschreiben, sind Hilfskonstruktionen nötig, nämlich die Definition eines Bezugssystems.
Die Bahnen, die sich den Teilchen in solch einem Bezugssystem zuordnen lassen, also die Angaben, wie sich für jedes Teilchen die Koordinatenwerte x,y,z für unterschiedliche Werte der Zeitkoordinaten verändern, sind eine weniger unmittelbare Beschreibung als die Angabe der Koinzidenzen. Die Liste der Koinzidenzen kommt ohne jegliche Hilfskonstruktionen aus.
Eine erste Forderung, die wir an physikalisch sinnvolle Bezugssysteme stellen müssen, ist daher, dass sie Koinzidenzen richtig wiedergeben: Wenn Ereignis E darin besteht, dass sich Teilchen A und Teilchen B treffen, dann sollten in einem vernünftigen Bezugssystem tunlichst bei dem betreffenden Ereignis beide Teilchen die gleichen Koordinatenwerte x(E), y(E), z(E) und t(E) haben.
Darüber hinaus erhebt unsere Definition von Bezugssystemen aber einen Anspruch auf allgemeinere Gültigkeit. Einmal definiert, soll unser Bezugssystem schließlich nicht nur eine Handvoll ausgewählter physikalischer Koinzidenzen richtig wiedergeben, jeweils von Fall zu Fall andere, sondern alle nur denkbaren solchen Koinzidenzen, egal, wo im Raum und zu welcher Zeit sie stattfinden.
Wir wollen uns schließlich nicht je nachdem, was gerade an konkreten Vorgängen abläuft – ob nun die Teilchen A und B hier kollidieren, oder aber die Teilchen C und D dort -, jeweils ein neues, direkt auf diese besondere Situation zugeschnittenes Bezugssystem definieren müssen.
Damit verallgemeinert sich unsere Forderung dahingehend, dass jedes sinnvolle Bezugssystem jedem möglichen Punktereignis E eindeutige Raumkoordinatenwerte x(E), y(E), z(E) und einen eindeutig definierten Zeitpunkt t(E) zuordnen muss, egal wo und zu welchem Zeitpunkt das Ereignis stattfindet.
Der Übergang vom einen Bezugssystem zum anderen
Aus der Eindeutigkeitsforderung folgt automatisch, dass es möglich sein muss, all die unterschiedlichen Bezugssysteme, die diese Forderung erfüllen, zueinander in Beziehung zu setzen.
Betrachten wir dazu außer unserem bereits definierten ersten Bezugsystem S ein zweites Bezugssystem S’ (gesprochen “S-Strich” oder “gestrichen S”). Nennen wir dessen Koordinaten um besserer Unterscheidbarkeit willen x’, y’, z’ und t’.
Dann sollte ein gegebenes Ereignis E in beiden Bezugssystemen eindeutige Koordinatenwerte haben: im Bezugssystem S die Koordinatenwerte x(E), y(E), z(E) und t(E), und im Bezugssystem S’ die Koordinatenwerte x'(E), y'(E), z'(E) und t'(E).
In geeigneten Einheiten – wir hatten Meter für die Längen- und Sekunden für die Zeitangaben gewählt – sind die vier Koordinatenwerte x(E), y(E), z(E), t(E) und ihre vier Entsprechungen x'(E), y'(E), z'(E), t'(E) sämtlich Zahlenwerte. Dass die Zuordnung der Koordinatenwerte zum Ereignis in beiden Fällen eindeutig ist – die gegebenen Koordinatenwerte x(E), y(E), z(E), t(E) bzw. x'(E), y'(E), z'(E), t'(E) beschreiben in dieser Kombination genau das Ereignis E, aber kein anderes – heißt, dass es eindeutige Zuordnungsregeln zwischen diesen beiden Vierergruppen von Zahlenwerten geben muss.
Anders gesagt: Wenn uns jemand die vier Zahlenwerte x(E), y(E), z(E), t(E) für das Bezugssystem S gibt, dann müssen wir aus diesen Werten eindeutig erschließen können, dass das Ereignis E gemeint ist – und dann iwederum können wir sofort sagen “…und im Bezugssystem S’ hat dieses selbe Ereignis die Koordinatenwerte x'(E), y'(E), z'(E), t'(E)”.
Wenn wir beispielsweise über ein Ereignis reden, das im Bezugssystem S in geeigneten Einheiten die Koordinatenwerte x(E)=4, y(E)=2, z(E)=3, t(E) = 120 hat, dann muss alleine diese Zahlengruppe (4,2,3,120) eindeutig beschreiben, um welches Ereignis es sich handelt, und welche andere Zahlengruppe demselben Ereignis im Bezugssystem S’ zugeordnet wird.
Mathematisch gesprochen heißt dies, dass es Funktionen gibt, die uns erlauben, die vier Koordinatenwerte x'(E), y'(E), z'(E), t'(E) direkt aus den vier Koordinatenwerten x(E), y(E), z(E), t(E) zu berechnen. Aus dem gleichen Grunde muss es umgekehrt Funktionen für die Bestimmung der x(E), y(E), z(E), t(E) aus den Koordinatenwerten x'(E), y'(E), z'(E), t'(E) geben.
Nennen wir die erstgenannten Funktionen e,f,g und h, dann gilt
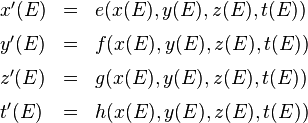
und für die Umkehrung gibt es Funktionen, die ich hier e’, f’, g’ und h’ nenne und für welche gilt 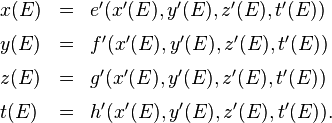
Die Gesamtheit der Funktionen e,f,g,h heißt Koordinatentransformation vom Bezugssystem S ins Bezugssystem S’.
Verkürzt kann man statt Koordinatentransformation auch einfach Transformation sagen, und wenn ersichtlich ist, dass S und S’ Bezugssysteme sind, kann es statt “…vom Bezugssystem S ins Bezugssystem S'” kürzer heißen “…vom System S ins System S'” oder, ganz kurz, “…von S nach S'”.
Die Funktionen e’, f’, g’, h’ definieren die Umkehrtransformation oder inverse Transformation, nämlich die Transformation von S’ nach S.
Die Transformationen von S nach S’ und jene von S’ nach S hängen in der folgenden Weise zusammen: Kenne ich die Koordinatenwerte x,y,z,t eines Ereignisses E im System S und berechne die Koordinatenwerte x’,y’,z’,t’ desselben Ereignisses im System S’, dann muss gelten: Benutze ich anschließend die Umkehrtransformationen von S’ nach S, um aus den x’,y’,z’,t’ Koordinatenwerte x,y,z,t zu berechnen, dann muss ich als Ergebnis genau wieder die Koordinatenwerte vom Anfang erhalten.
Nützliche Kurzschreibweisen
Im Umgang mit den Koordinaten von Ereignissen hat sich eine nützliche Kurzschreibweise eingebürgert. In den vorangehenden Abschnitten hatte ich unterschieden zwischen den Koordinaten x, y, z, t als Funktionen (anders ausgedrückt: als Zuordnungsvorschriften) einerseits und den spezifischen Koordinatenwerten x(E), y(E), z(E) und t(E) die einem konkreten Ereignis zugeordnet waren, andererseits.
In der Physik hat sich für beides die gleiche Schreibweise eingebürgert. x, y, z sind weiterhin allgemeine Zuordnungsvorschriften, aber wir benutzen die gleichen Buchstaben auch für Koordinatenwerte und reden beispielsweise darüber, das Ereignis E habe die Koordinatenwerte x = 2, y=3, z=1 und t = 3600. Solange man jeweils auf den Zusammenhang achtet, sollte diese Kurzschreibweise nicht zu Missverständnissen führen.
Auch die letzten beiden Viererpackungen von Formeln für die Koordinatentransformationen sind recht schreibintensiv. Ich musste zusätzliche Namen für die Funktionen einführen, und die wiederholte Erwähnung von E machte die Formeln ebenfalls recht länglich. Daher hat sich eine Kurzschreibweise eingebürgert, in der man für Transformationsfunktionen einfach die Symbole der entsprechenden Koordinaten verwendet und auch hier nicht mehr überall explizit dazu schreibt, dass sich die Gleichungen auf Koordinaten für jeweils ein und dasselbe Ereignis E beziehen.
Die Transformation von S nach S’ schreibt sich dann einfach
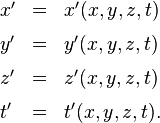
Sobald eine explizite Form für die Funktionen gefunden ist, steht dann auf der rechten Seite nur noch ein Ausdruck, in dem x, y, z und t und in der Regel noch einige die Transformation charakterisierende Parameter vorkommen. Bei einer Transformation, in der das eine System gegenüber dem anderen in x-Richtung um die Strecke a verschoben ist, steht dort beispielsweise
Die Umkehrtransformation von S’ nach S ist in dieser Schreibweise
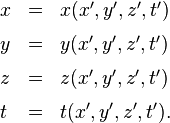
Auch diese Kurzschreibweise sollte nicht zu Missverständnissen führen, solange man sich bei Transformationsausdrücken immer klar macht, was sie aussagen: Sind x,y,z,t die Koordinatenwerte im Bezugssystem S eines ganz bestimmtes Ereignisses E, dann liefern diese Funktionen die Koordinaten x’, y’,z’,t’ desselben Ereignisses im Bezugssystem S’. Bei Rechnungen, die solche Formeln benutzen, müssen sich x,y,z,t und x’,y’,z’,t’ jeweils auf dasselbe Ereignis beziehen; anders ergeben die Kurzformeln keinen Sinn.
Prime-Zeichen und gestrichene Systeme
Eine weitere nützliche Konvention habe ich in den vorangehenden Abschnitten bereits verwendet: Vergleicht man verschiedene Bezugssysteme, dann bezeichnet man sie oft als S, S’, S” mit unterschiedlicher Anzahl von Strichen (typografisch gesprochen handelt es sich bei diesen Strichen um Prime-Zeichen).
Das System S’ heißt dann auch gestrichenes System, S” heißt zweifach gestrichenes System, und so weiter. Kommt man irgendwo in die Verlegenheit, vier oder mehr gestrichene Systeme einführen zu müssen, ist auch die Schreibweise
![]()
eine Möglichkeit. Dabei werden ab dem vierfach gestrichenen System (oder danach) nicht mehr all die Striche hingemalt, sondern stattdessen als Index eine vier in Klammern. Das kommt aber nur sehr selten vor.
Die Schreibweise mit den Strichen hat den Vorteil, dass sie sich auf alle Größen übertragen lässt, die zu den behandelten Bezugssystemen gehören: ist x die x-Koordinate (z.B. eines bestimmten Ereignisses) des S-Systemes, dann bezeichnet x’ die entsprechende Größe bezogen auf S’ (die x’-Koordinate desselben Ereignisses) und so weiter, und genau so geht es mit ungestrichenen, zwei- der noch mehrfach gestrichenen Größen.
Das ist eine übersichtliche Art und Weise, Systeme und die darauf bezogenen Größen zu unterscheiden und mit einem Blick zu sehen, auf welches von mehreren Bezugssystemen sich eine bestimmte Angabe bezieht. Selbst wenn man einmal überlesen haben sollte, was eine bestimmte, mit einem Strich versehene Größe darstellt – alleine der Strich sagt einem dieser Konvention gemäß, dass sich die betreffende Größe auf das Bezugssystem S’ bezieht.
Beobachter und Bezugssysteme
Eine weitere Gewohnheit der Physiker besteht darin, die Bezeichnungen Bezugssystem S und in S ruhender Beobachter (verkürzt Beobachter in S oder gar Beobachter S) weitgehend synonym zu verwenden.
Eine Aussage wie “Ein Beobachter in S misst für das Ereignis E den x-Koordinatenwert 2” ist dann gleichwertig zu “Der x-Koordinatenwert von E im Bezugssystem S ist 2”. Das ist lediglich eine Abkürzung und bringt zudem etwas größere Flexibilität bei der sprachlichen Beschreibung dessen, was da vorgeht.
Der Beobachter, der damit gemeint ist, ist oft genug nur eine nützliche Fiktion – es kann sein, dass solch ein Beobachter auf Teilchen reiten, im Zentrum der Sonne ruhen und derlei anderer in Wirklichkeit unmöglicher Dinge mehr tun müsste. In Situationen, in denen er doch einem realen Beobachter entspricht, sollte das, was der reale Beobachter feststellt und misst, allerdings tunlichst dem entsprechen, was da in verkürzter Form ausgesagt wurde!
Diese Verwendung des Wortes Beobachter weicht an einer Stelle vom Alltagssprachgebrauch ab. Tatsächliche Beobachter aus Fleisch und Blut, sprich: die Wissenschaftler, die Beobachtungen anstellen, können durchaus außerhalb des Bezugssystems agieren, in dem sie selbst ruhen, und dort, wo es nützlich ist, ein ganz anderes Bezugssystem verwenden, um ihre Beobachtungen zu beschreiben und einzuordnen.
Ein gutes Beispiel sind die Astronomen, die ihre Messungen oft ganz selbstverständlich in Bezugssystemen ausdrücken, in denen weder sie selbst noch ihre Teleskope ruhen. Das äquatoriale Koordinatensystem für Himmelskörper ist ein spezielles Beispiel, das relativ zum Schwerpunkt des Sonnensystems ruhende Bezugssystem zur Berechnung von Bewegungen im Sonnensystem ein weiteres.
Wo im Zusammenhang mit den Relativitätstheorien von Beobachtern die Rede ist, muss man daher etwas auf der Hut sein: Ist das Wort Beobachter dort nur ein Synonym für “Bezugssystem”? Oder ist ein Beobachter im Alltagssinn gemeint? Ich werde mich im folgenden bemühen, dass jeweils auf dem Zusammenhang klar wird, welche Bedeutung in jedem konkreten Falle gemeint ist.
Eine weitere Unterscheidung im Zusammenhang mit dem Beobachter-Begriff wird später ebenfalls noch wichtig. Oft werden die Aussagen, dass ein Beobachter etwas “sieht”, “beobachtet”, “misst” oder “feststellt” synonym verwendet. Tatsächlich gibt es da aber zwei sehr unterschiedliche Fälle.
Was ein Beobachter zu einem gegebenen Zeitpunkt tatsächlich sieht, hängt davon ab, wieweit der Beobachter von dem beobachteten Ereignis entfernt ist: Sehen heißt, dass das Licht in dem betreffenden Zeitpunkt bei dem Beobachter eintrifft. Da Licht aber eine gewisse Zeit benötigt, um von einem Ort zum anderen zu gelangen, ist das, was ein Beobachter sieht, bereits vorbei – wenn der Beobachter einen bewegten Körper sieht, dann ist der betreffende Körper, bis sein Licht den Beobachter erreicht hat, bereits seinerseits ein Stück weitergeflogen.
Auch diese Unterscheidung sollte man sich einmal klar machen, damit es nicht zu Missverständnissen kommt. Wenn im Hinblick auf ein Bezugssystem Ausdrücke wie “aus Sicht des Systems S’ gilt…” fallen, ist dagegen mit großer Sicherheit nicht gemeint, dass es tatsächlich um einen Sehvorgang samt den erwähnten Verzögerungseffekten geht. “Aus Sicht des Systems S’ bewegt sich der Körper mit Geschwindigkeit v” ist nur eine andere Ausdrucksweise für “Im/bezogen auf das Bezugssystem S’ bewegt sich der Körper mit Geschwindigkeit v”.
Erste Folgerungen aus den Transformationen
Zurück von den Konventionen und Schreibweisen zu dem, was die Transformationsfunktionen an Informationen enthalten. Leser, denen die hier angestellten Überlegungen allzu abstrakt vorkommen, mögen beruhigt sein: Wir werden das, was hier gesagt wird, später anhand der konkreten Beispiele noch einmal aufgreifen. Aber es ist durchaus nützlich, sich zunächst einmal Gedanken darüber zu machen, was sich bereits aus dem Umstand ergibt, dass es überhaupt Transformationsfunktionen gibt.
Die Transformationsfunktionen, die wir eingeführt hatten, betreffen zunächst einmal die Koordinaten von einzelnen Ereignissen E. Für jedes Ereignis E können wir, gegeben dessen Koordinaten x,y,z,t im Bezugssystem S, die Koordinaten x’,y’,z’,t’ desselben Ereignisses im Bezugssystem S’ berechnen, und umgekehrt.
Gleichzeitigkeit
Eine allgemeine Aussage, die sich direkt aus den Transformationen ableiten lässt, betrifft die Gleichzeitigkeit. Betrachten wir zwei Ereignisse E und F, die im ungestrichenen System S gleichzeitig stattfinden, anders ausgedrückt: Im Bezugssystem S wird beiden Ereignissen derselbe Zeitkoordinatenwert zugeordnet, t(E) = t(F).
Aus den Transformationsfunktionen können wir dann ableiten, ob die Ereignisse auch im gestrichenen System gleichzeitig stattfinden. Dabei spielen im allgemeinen auch die Orte beider Ereignisse eine Rolle, denn um anhand der Transformationsfunktion
den Zeitkoordinatenwert t’ zu bestimmen, der einem Ereignis E im System t zugeordnet wird, müssen wir auf der rechten Seite eben nicht nur t(E) einsetzen, sondern ebenso die Raumkoordinaten x(E), y(E), z(E) des Ereignisses im System S.
Analog gehen wir vor, um t'(F) zu berechnen. Der Vergleich von t'(F) und t'(E) zeigt dann, ob beide Ereignisse auch im Bezugssystem S’ gleichzeitig stattfinden.
Für die Transformationen, die man in der klassischen Mechanik betrachtet, wird das der Fall sein; in der Speziellen Relativitätstheorie dagegen wird sich Gleichzeitigkeit bei Übergängen von einem Bezugssystem zum anderen im allgemeinen ändern (“Relativität der Gleichzeitigkeit”).
Zeitintervalle
Betrachten wir als nächstes eine Uhr, die im System S ruht. Die Uhr möge mit der in S definierten Zeitkoordinate synchronisiert sein, also zu jedem Zeitpunkt t auch genau den Wert t anzeigen. Dass die Uhr in S ruht, bedeutet, dass ihre Ortskoordinaten im Bezugssystem S konstant sind, sagen wir: x=a, y=b, z=c.
Aus
![]()
einem Ausdruck, der in diesem Falle (Einsetzen der konstanten Koordinatenwerte) die einfache Form
![]()
annimmt, können wir dann direkt ablesen, zu welchen Zeitpunkten im System S’ die verschiedenen Anzeigen der Uhr stattfinden.
Nehmen wir als Beispiel die zwei Ereignisse “Uhr zeigt t=0 an” und “Uhr zeigt t= eine Sekunde an”. Für jedes dieser Ereignisse können wir die zugehörige t’-Koordinate berechnen und anschließend feststellen, ob im System S’ gemessen an der in S’ definierten Zeitkoordinate t’ mehr Zeit als eine Sekunde vergangen ist, genau eine Sekunde, oder weniger als eine Sekunde.
Dazu müssen wir nur die Differenz zwischen
und
bilden, die anzeigt, wieviel Zeit zwischen den beiden Uhrenanzeigen vergangen ist, gemessen anhand der in S’ gültigen Zeitkoordinate. So können wir die Zeitmessung in beiden Systemen zueinander in Beziehung setzen.
In der klassischen Mechanik stellt sich heraus, dass solche Zeitkoordinatendifferenzen oder Zeitintervalle in beiden Systemen immer die gleichen sind: Zwischen der Anzeige “0 Sekunden” und “1 Sekunden” läuft auch die Zeitanzeige jedes der Bezugssysteme in der klassischen Mechanik genau eine Sekunde weiter.
In der Speziellen Relativitätstheorie dagegen wird sich zeigen, dass es im allgemeinen durchaus vom Bezugssystem abhängt, welches Zeitintervall zwischen zwei Ereignissen E und F vergeht. Zwar wird das Zeitintervall, gemessen in dem System, in dem die Uhr ruht, nach wie vor mit dem übereinstimmen, was die Uhr anzeigt. In Bezugssystemen, relativ zu denen sich die Uhr bewegt, wird das aber nicht mehr der Fall sein. Den zugehörigen Effekt der Zeitdilatation werden wir in einem späteren Beitrag noch genauer kennenlernen.
Die Transformation von Bahnkurven
Beschreiben wir im Rahmen der klassischen Mechanik die Bewegungen von Körpern, dann jeweils als Bahnen im Raum: im Bezugssystem S entspricht das der Angabe von Funktionen x(t), y(t), z(t) für die drei Ortskoordinaten des Körpers (bei ausgedehnten Körpern z.B. Ortskoordinaten für den Schwerpunkt) in Abhängigkeit von der Zeitkoordinate t des Systems.
Wie sich die Werte von x(t), y(t) und z(t) je nach eingesetzter Zeit t ändern, beschreibt, wie sich der Körper mit der Zeit durch den Raum bewegt. Sind diese drei Funktionen gegeben, lassen sich auch die Geschwindigkeit des Körpers und seine Beschleunigung angeben: Die Geschwindigkeitskomponenten in x-, y- und z-Richtung sind die Änderungsraten (Ableitungen) der Funktionen x(t), y(t) bzw. z(t) mit der Zeit, und die Beschleunigungen in x-, y- und z-Richtungen die Änderungsraten (Ableitungen) der Geschwindigkeitskomponenten mit der Zeit.
Wie sieht es mit der Bahn desselben Körpers im gestrichenen System S’ aus? Die lässt sich in zwei Schritten berechnen. Setzen wir x(t), y(t) und z(t), also die Bahn des Körpers, ausgedrückt in den Koordinaten des Bezugssystems S, in die Transformationsformel
![]()
ein, dann steht dort
![]()
mithin also eine Gleichung, in der auf der linken Seite t’ steht und auf der rechten Seite als einzige freie Variable nur noch t vorkommt.
Löst man diese Gleichung nach t auf, dann erhält man einen entlang der Bahnkurve des Körpers gültigen Zusammenhang t(t’), sprich: t als eine Funktion der t’-Koordinate des Systems S’. Damit wiederum kann man sich die Gleichungen für x’, y’ und z’ vornehmen: Setzt man in
![]()
auf der rechten Seite die Bahn x(t), y(t), z(t) ein, dann hat man immerhin schon eine Gleichung, die nur noch von t abhängt, also zusammenfassend geschrieben werden kann
![]()
Setzen wir jetzt noch den zuvor abgeleiteten Zusammenhang t(t’) ein, der für alle Ereignisse auf der Bahnkurve des Körpers gilt, und schon haben wir, wie gewünscht, den Zusammenhang
![]()
nämlich die Aussage, wie sich die im System S’ gemessene x’-Koordinate des Körpers mit der in S’ gemessenen Zeit t’ ändert.
Das ist bereits ein Drittel der gesuchten Bahngleichung des Körpers im System S’. Ganz analog können wir für y’ und z’ vorgehen.
Haben wir die drei Bahnfunktionen x'(t’), y'(t’) und z'(t’) bestimmt, dann können wir über die Änderungsrate und über deren Änderungsrate – die Ableitung erfolgt diesmal natürlich nach der Zeitkoordinate t’ – die Geschwindigkeit des Körpers und seine Beschleunigung im System S’ berechnen.
Hat man solchermaßen eine Möglichkeit, Bewegungen, Geschwindigkeiten und Beschleunigungen zu bestimmen, kann man auf die gleiche Weise, wie wir das im System S getan haben, Massen bestimmen (mit einer baugleichen Hooke’schen Feder wie der im System S), dann Kraftstärken, und so weiter. Auf diese Weise kann man im Prinzip alle Gesetze der Mechanik herausfinden, in derjenigen Form, in der sie im System S’ gelten.
Längen
Betrachten wir als letztes einen in S ruhenden Körper, dessen Länge wir bestimmen wollen, etwa einen langen Stab. Da es uns nur um die Länge geht, vernachlässigen wir Breite und Tiefe des Stabes und betrachten den Stab als eindimensionales Gebilde mit einem Anfangspunkt, einem Endpunkt und einer geraden Verbindung zwischen den beiden.
Dass der Stab relativ zum Bezugssystem S ruht, bedeutet, dass die Koordinaten seines Anfangspunkts in diesem System konstante Werte haben, und dass die Koordinaten seines Endpunkts konstante Werte haben. Nehmen wir an, der Anfangspunkt des Stabes befindet sich bei x=a, y=b, z=c, wobei a,b,c die konstanten Werte für die Koordinaten sein sollen, und der Endpunkt bei x=d, y=e, z=f.
In einem zweiten Bezugssystem S’ können sich die Koordinatenwerte, die Stabanfang und -ende zugeordnet werden, durchaus mit der Zeit ändern. Die verschiedenen Bahnfunktionen x'(t’), y'(t’), z'(t’) für Anfangs- und Endpunkt hängen dann von der Zeitkoordinate t’ ab; je nachdem, zu welcher Zeit man misst, befindet sich der Stab im System S’ an einem anderen Ort.
Die Bahnfunktionen kann man in diesem einfachen Fall wiederum recht direkt bestimmen, wenn man die Transformationsfunktionen kennt. Wir führen diejenigen Schritte durch, die wir bei der Transformation von Bahnkurven ausgeführt hatten: Aus der Gleichung
![]()
die in diesem Falle (Einsetzen der konstanten Koordinatenwerte) wieder die einfache Form
![]()
annimmt, können wir durch Auflösen nach t eine für alle Ereignisse entlang der Bahn gültige Abhängigkeit des Wertes von t vom Wert für t’ ableiten, eine Funktion t(t’). Ich schreibe diese Funktion als tA(t’), wobei der Index A darauf hinweisen soll, dass diese Beziehung nur für Ereignisse auf der Bahn des Anfangspunkts des Stabs gilt. Für den Endpunkt kann man analog eine Beziehung tE(t’) ableiten.
Daraus und aus den allgemeinen Transformationen kann man für jeden Zeitpunkt t’ berechnen, wo sich der Anfangspunkt des Stabes im System S’ befindet und wo der Endpunkt des Stabes. Für die Koordinaten des Anfangspunkts in Abhängigkeit von der S’-Zeitkoordinate t’ findet man
für die Koordinaten des Endpunkts entsprechend
Den Abstand von Anfangs- und Endpunkt erhält man, wenn man zu ein und demselben Zeitpunkt t’ den dreidimensionalen Satz des Pythagoras anwendet, nämlich als
Wenn der Stab auch im gestrichenen System eine gerade Verbindung zwischen Anfang- und Endpunkt bildet, dann ist das Ergebnis die Länge des Stabs, gemessen im System S’. Das wird in den Beispielen für Transformationen, die wir später betrachten, in der Tat der Fall sein.
Ein wichtiger Aspekt dieser Formel ist, dass die Position von Anfang- und Endpunkt zum gleichen Zeitpunkt t’ bestimmt werden, bevor man aus den Koordinaten die Länge berechnet.
Das wird wichtig, sobald sich der Stab relativ zu dem System S’, in dem seine Länge bestimmt werden soll, bewegt. Warum, das ist in den folgenden Abbildungen/Animationen veranschaulicht.
Die Länge eines Stabes kann man messen, indem man den Anfang des Stabs an den Nullpunkt eines Maßstabs legt und abliest, bei welcher Markierung das Ende zu liegen kommt. In diesem Beispiel hier ist der lilafarbene Stab offenbar 8 Zentimeter lang:
Die Raumkoordinaten, die wir eingeführt haben, sind so definiert (siehe Teil I), dass sie genau solch eine Länge reproduzieren – die Länge, die ich bekomme, wenn ich für einen in S’ ruhenden Stab die Raumkoordinaten x’A, y’A, z’A des Anfangs- und x’E, y’E, z’E des Endpunkts bestimme und dann mit dem dreidimensionalen Satz des Pythagoras
deren Distanz ausrechne, muss das gleiche Ergebnis wie bei direkter Messung mit einem Maßstab. Den Vergleich mit den Markierungen eines Maßstabs kann man auch vornehmen, wenn sich das Objekt, dessen Länge es zu messen gilt, am Maßstab vorbeibewegt.
Man muss freilich darauf achten, dass man die beiden Teile der Messung (erstens feststellen, dass der Anfangspunkt des Objekts gerade am Nullpunkt des Maßstabs liegt; zweitens ablesen, an welcher Markierung des Maßstabs der Endpunkt des Objekts liegt) gleichzeitig vornimmt, wie hier gezeigt:
Nimmt man nämlich beispielsweise das Ablesen am Endpunkt des Objekts zu spät vor, dann bekommt man ein zu großes Ergebnis für die Länge:
Nimmt man das Ablesen am Endpunkt dagegen zu früh vor, dann bekommt man umgekehrt ein zu kleines Ergebnis für die Länge. Daher ist das gleichzeitige Ablesen wichtig. Und da Gleichzeitigkeit im System S’ gleichen Werten der Zeitkoordinate t’ des Systems entspricht, haben wir in der obigen Formel für d'(t’) Anfangs- und Endkoordinaten zur gleichen Zeit ausgewertet.
In der klassischen Mechanik haben solche Überlegungen keinerlei praktische Konsequenzen. Dort ist, wie schon erwähnt, Gleichzeitigkeit für alle Systeme dasselbe. In der Speziellen Relativitätstheorie dagegen trägt die Berücksichtigung der Gleichzeitigkeit zu einem Effekt bei, demzufolge die Länge eines Stabs je nach Bezugssystem unterschiedliche Werte annimmt – der sogenannten Längenkontraktion.
Aber das ist an dieser Stelle noch Zukunftsmusik. Eine Reihe wichtiger – wenn in diesem Teil auch notwendiger Weise noch abstrakter – Informationen, die man aus Koordinatentransformationsformeln gewinnen kann, haben wir jetzt vorgestellt. Es wird Zeit, konkrete Beispiele für Bezugssystemwechsel anzuschauen – das ist das Thema von Teil VII: Bezugssystemwechsel in der klassischen Mechanik.
Wie für die vorangehenden Teile von “Einstein verstehen” gilt auch für diesen hier, dass ich Veränderungen, die sich aus der hier geführten Diskussion ergeben, direkt umsetzen werde. Die Originalfassung habe ich zum Vergleich hier als PDF eingestellt.
Meinen Umgang mit Kommentaren in diesem Blog habe ich in diesem Blogbeitrag erläutert. Inbesondere gilt: Der obige Text stellt den sechsten Schritt einer systematischen Einführung in die Spezielle Relativitätstheorie dar; die Diskussion sollte auf den hier behandelten Themenbereich beschränken und insbesondere nicht auf das vorgreifen, was erst in den nachfolgenden Teilen der Einführung angesprochen wird. Ich behalte mir vor, Diskussionsbeiträge, die dem Leser keinen Mehrwert bieten, sondern die Diskussion stören, zu löschen.
Die Kommentare können zwischenzeitlich moderiert sein und werden dann von mir jeweils erst freigeschaltet. Daher bitte Geduld, wenn Sie einen Kommentar eingestellt haben, dieser aber nicht gleich unten auf dieser Seite erscheint!


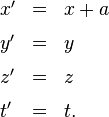
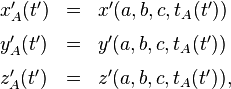
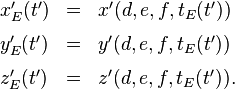



„Nimmt man nämlich beispielsweise das Ablesen am Endpunkt des Objekts zu spät vor, dann bekommt man ein zu großes Ergebnis für die Länge:“
Normalerweise würde ich es ja für absolut selbstverständlich betrachten, dass man die Markierungen bei der Längenmessung eines bewegten Objektes gleichzeitig im “Ruhesystem” anbringt.
Eingefleischten “SRT-Kritikern” lässt sich dies allerdings kaum vermitteln!
Deswegen zur Auflockerung hier mal was Lustiges aus “Trollhausen”
http://www.mahag.com/neufor/viewtopic.php?f=6&t=624&start=50
…unter anderem deswegen fange ich ja so weit vorne an, bei der klassischen Mechanik, bzw. hier bei allgemeinen Schlussfolgerungen aus Transformationen. Weil vieles von dem, was sich da an Missverständnissen ergibt, bereits auf so einfacher Ebene liegt und zunächst einmal gar nichts mit dem zu tun hat, was später dann für die Spezielle Relativitätstheorie spezifisch ist.
Ich hab auch den folgenden Trompe-l’œil im obenstehenden Text genossen und möcht das hier mitteilen ohne so vermessen zu sein, nun zu meinen, es handle sich um einen Primeur:
S’ unmittelbar gefolgt von ” sieht auf den ersten Blick aus wie ein dreigestrichenes S, also ein S mit drei Prime’s. Das kann allerdings nur für diejenigen zum Missverständnis führen, die Texte über physikalische und mathematische Sachverhalte genau gleich lesen wie Zeitungstexte. Etwas was man sich schnell abgewöhnen sollte.
…nach kurzem Abwägen habe ich mich aber doch entschlossen, den Augentäuscher zu entschärfen.
Ich habe starke Schwierigkeiten zu entscheiden, wann sie vom Modell sprechen und wann von der Realität. Das beginnt z.B. bei Punkt, Raum-Punkt, Zeit-Punkt, Idealisierter Punkt, Punkt-Ereignisse, Null-Punkt, End-Punkt. Welcher “Punkt”-Begriff gilt für die reale Welt und welcher für das (mathematischen) Modell. Aus meiner Sicht ein für Anfänger sehr schwer zu verstehender Text.
“Kommen wir zur Zeit: Jedem Moment/Augenblick/Zeitpunkt T können wir in unserem Bezugssystem einen eindeutigen Zeitkoordinatenwert t(T) zuordnen. Auch ein solcher Zeitpunkt ist freilich eine Idealisierung – in unserem mathematischen Modell der Zeit, der Zeitgeraden, entspricht er einem Punkt auf der Geraden.”
Hier exemplarisch: Es ist ein ständiger begrifflicher Ebenenwechsel zwischen den Worten, Moment (=Real), Augenblick (=Real), Zeitpunkt T (=Modell), Bezugssystem (hm, doch alles was vorher stand =Modell?, oder ist ein reales Bezugssystem gemeint?), Zeitkoordinate (=vom Modell?), Zeitpunkt ist Idealisierung (ok, also war vorher doch die reale Zeit-Koordinate gemeint, wovon jetzt idealisiert wird?), Mathem. Modell (=Modell), Zeit (=Real, aber jetzt weiß man wieder nicht, ob sich die vorherigen Worte in denen sie “Zeit” verwenden, das Modell oder die reale Zeit bezeichnen, oder Idealisieren sie von einer Idealisierung?), Zeitgerade (=Modell), Punkt auf Geraden (=Modell).
Hm. Ich sehe das Problem und muss noch etwas überlegen, wie ich das klarer ausdrücken kann. Zum einen will ich in meinem Text den Unterschied Wirklichkeit/Modell deutlich machen, zum anderen aber nicht zu tief in die Details abtauchen. “Zeitpunkt” ist bereits vom Alltagsgebrauch verwirrend – mathematische Punkte gibt es in der Wirklichkeit ja nun schon einmal gar nicht.
Ich möchte noch 2 Sachen ergänzen:
Ein interessierter Anfänger (also jemand der schon recht viel über RT gelesen und gehört hat, aber es jetzt endlich mal richtig verstehen will), kommt natürlich mit einem impliziten Verstehens-“Ballast” an Wörter, die bereits mit (leider synaptisch ziemlich stabilen) Vorstellungen verknüpft sind. Zum Beispiel das Wort “Bezugssystem”. Hier tauchen so gut wie immer “Raumschiffe”, “Zwillinge”, “Erde”, “Eisenbahnen”, “Bahnsteige” und “Fahrstühle” auf (also reale Dinge). Jetzt kommt derjenige zu Ihnen und hat m.E. Schwierigkeiten auf die Schnelle zw. dem realen Bezugssystembegriff und dem mathematischen (Modell-)Bezugssystembegriff hin- und her zu springen (weil das Wort “Bezugssystem” ebenen-mäßig sozusagen doppelt verwendet wird). Auch ist es nicht eindeutig zu verstehen wenn sie schreiben “wir wechseln in ein anderes Bezugssystem”, ob sie dann meinen, wir wechseln von der Eisenbahn zur Mathematik oder von der Eisenbahn zur anderen Eisenbahn, oder von Mathemodell1 zu Mathemodell2.
Ich habe mal zum Wort “Punkt” alle Wort-Erweiterungen herausgesucht: Raum-Punkt, Zeit-Punkt, Raumnull-Punkt, Null-Punkt, Punkt-Förmig, Idealisierter Raum-Punkt, Eck-Punkt, Punkt-Förmige Kügelchen, Punkt auf Gerade, Punkt-Ereignis, Punkt-Teilchen, End-Punkt des Objekts + ähnlich/gleich gemeinte Worte: Raumkoordinate, Ort P, Kartesische Koordinate, Ortskoordinate, Ort, Raumkoordinatenwert, Moment, Augenblick, Zeitkoordinatenwert, Idealisierter Zeitpunkt
Noch eine Anmerkung: Die Begriffserklärung zum sehr anfänger-ungewohnten Wort “Koinzidenzen” ist nicht gut verständlich.
Sorry, wenn ich leider nur Kritik im Gepäck habe, aber ich versuche selbst anderen die Grundlagen und Grundbegriffe der Mathematik zu erklären und da schaue ich halt immer recht didaktisch-kritisch 😉
Ich habe mal vor einiger Zeit bei ” Einstein verstehen: Ein Blogexperiment, Teil I ” (ganz unten) zwei Kommentare gepostet, leider aber keine Antwort erhalten, ich ziehe das mal als Zitat hier rein:
Sie: “Im euklidischen Raum der Mathematik ist dagegen jeder Punkt im Raum wohldefiniert – der Raum ist lückenlos mit Punkten “gefüllt.”
Ich: Verwenden sie “wohldefiniert” i.S. des allg. Sprachgebrauches oder i.S. der Mathematik? Mathematisch richtig ist: “definiert” Der Begriff „wohldefiniert“ passt nicht, sonst müsste die Frage lauten: Welche Eigenschaft des Raumes soll durch einen (einzelnen) Punkt definiert werden? „wohldefiniert“ ist nicht die Steigerung von „definiert“. Also nicht => definiert, gut definiert, noch besser definiert, am allerbesten definiert, wohldefiniert. Der Begriff „definiert“ passt (strenggenommen) für einen axiomatischen Grundbegriff eigentlich auch nicht. Eher noch: „implizit definiert“.
Nachzulesen z.B. bei Beutelsbacher, im Buch o.B.d.A. trivial
“Wohldefiniert” war in der Tat nicht die richtige Wortwahl. Ich bin nicht sicher, den Kommentar da überhaupt gesehen zu haben (damals gab’s keine automatische Benachrichtigungen, und ich habe bei den alten “Einstein verstehen”-Teilen nicht sehr häufig nachgeschaut – sorry). Ist jetzt jedenfalls geändert.
Die Anregung, hier schon an die späteren Standardbeispiele wie Raumschiff, Zwilling etc. anzuknüpfen, ist ebenfalls gut. Ich schaue gerade, wieviel Änderungsbedarf das für den vorliegenden Text – der derzeit noch eine etwas andere Stoßrichtung hat – bedeutet.
So, jetzt ist der erste Teil etwas umgeschrieben. Das ist immer ein Balanceakt zwischen mathematisch (bzw. philosophisch) exakter Ausdrucksweise und einfach lesbarem Text, aber jetzt sind zumindest Modell und Wirklichkeit besser voneinander abgesetzt – hoffentlich ohne den Text dadurch zuviel komplizierter zu machen.
Markus Pössel schrieb (25. Dezember 2013):
> In der Speziellen Relativitätstheorie […] wird sich zeigen, dass es im allgemeinen durchaus vom Bezugssystem abhängt, welches Zeitintervall zwischen zwei Ereignissen E und F vergeht.
Man darf gespannt sein, ob und welche Aussagen zum (sog. “invarianten”) Intervall zwischen zwei bestimmten zueinander zeitartigen Ereignissen in dieser “Online-Einführung in die Spezielle Relativitätstheorie” noch getroffen werden.
(Vielleicht würde dabei ja sogar Terminologie benutzt bzw. anerkannt, mit deren Hilfe sich die Fragen um so eindringlicher stellen ließen, die von den vorausgegangenen “Teilen” her noch unbeantwortet sind.)
@Markus Pössel
Da scheint mir Frank Wappler berechtigt ein Haar in der Suppe zu beanstanden (»In der Speziellen Relativitätstheorie […] wird sich zeigen, dass es im allgemeinen durchaus vom Bezugssystem abhängt, welches Zeitintervall zwischen zwei Ereignissen E und F vergeht.«)
Eine kartographische Analogie dazu wäre ungefähr so:
“Im allgemeinen hängt es durchaus von der Weltkarte ab, wie gross Grönland ist. Den zugehörigen Effekt der Grönland-Dilatation werden wir noch genauer kennenlernen.”
Die Kritik und die Analogie kann ich nicht nachvollziehen.
Sowohl in der klassischen Mechanik als auch in der Speziellen Relativitätstheorie betrachtet man schließlich nicht alle möglichen Transformationen, sondern nur ganz bestimmte, nämlich solche zwischen Bezugssystemen, die die Geometrie des Raums (angenommen als Euklidischer Raum) und den Gang im Bezugssystem ruhender Uhren (baugleich etc.) richtig wiedergeben.
Das ist eine beachtliche Einschränkung, und in der klassischen Mechanik wird ja angenommen, dass Zeitintervalle und räumliche Distanzen in solchermaßen definierten Bezugssystemen in der Tat invariant sind. Dass es in der Speziellen Relativitätstheorie nicht so ist, ist durchaus bemerkenswert und auch anmerkenswert.
In der SRT wird eine relative Größe (Geschwindigkeit) zu einer absoluten Größe gemacht. Selbstverständlich dass dadurch die absoluten Größen (Länge, Zeit) relativiert werden.
Nein, es gibt eine Maximalgeschwindigkeit ohne additiv Inverse.
Das wird (hoffentlich) klar, wenn wir dann bei der SRT angekommen sind. An dieser Stelle ist es noch ein Vorgriff.
@Markus Pössel
Ein Zeitintervall zwischen zwei Ereignissen E und F ist letztlich doch zu ermitteln mit einer Uhr, die von E nach F bewegt wird, und hängt nur ab vom Weg, den die Uhr dazwischen nimmt. Das ist dann völlig unabhängig vom Bezugssystem. Wenn Zeitintervalle jetzt aber als abhängig vom Bezugssystem angekündigt werden, dann wird dieser Eindruck hinterher irgndwann wieder zu korrigieren sein, was sich durch eine andere Formulierung vermutlich vermeiden liesse,
Genaugenommen misst im allgemeinen Fall die “Zeit” t eines Bezugssystem S ja auch nicht ein Zeitintervall zwischen den Ereignissen E und F, sondern vielmehr eines zwischen zwei Ereignissen P(E) und P(F), die aus Sicht von S jeweils gleichzeitig sind zu E bzw. F, und die in S erhalten werden können durch orthogonale Projektion von E bzw. F auf eine beliebige t-Koordinatenlinie. Und gemessen wird dann mit einer in S “ruhenden” Uhr, deren Weltlinie gerade dieser t-Koordinatenlinie entspricht. Wir haben es also bezogen auf ein Koordinatensystem im allgemeinen mit der Vermessung eines projizierten Intervalls zu tun, welches dann vielleicht nicht mehr so ohne weiteres als »Zeitintervall zwischen E und F« bezeichnet werden sollte.
In meinem Text ist mit Zeitintervall schlicht die Zeitkoordinatendifferenz gemeint; dass bereits der Begriff “Intervall” in der Speziellen Relativitätstheorie so eng an Eigenzeitmessungen gekoppelt wäre, dass man ihn für nichts anderes mehr verwenden dürfte, wäre mir neu.
Dass die Zeitkoordinatendifferenz bei zwei Ereignissen von Bezugssystem zu Bezugssystem variiert, ist angesichts unserer Alltagserfahrungen bemerkenswert bzw. anmerkenswert genug.
Auf den invarianten Hintergrund (Projektionen etc.) werden wir sicher auch noch kommen, aber das ist noch einen Schritt weiter von unserer Alltagserfahrung entfernt.
Markus Pössel schrieb (28. Dezember 2013 13:20):
> […] dass man ihn [den Begriff “Intervall”] für nichts anderes mehr verwenden dürfte, wäre mir neu.
Das, was man (begrifflich) zu unterscheiden imstande ist, sollte man ja konsistent mit verschiedenen Worten benennen, um sich verständlich auszudrücken.
> […] dass bereits der Begriff “Intervall” in der Speziellen Relativitätstheorie so eng an Eigenzeitmessungen gekoppelt wäre
Schon mal erfreulich (besonders für Physiker, allerdings auch für Nichphysiker), wenn Messungen von anderen Methoden unterschieden werden können, reelle (Verhältnis-)Zahlen hervorzurufen.
Die Messung eines Intervalls zwischen zwei bestimmten (zueinander zeitartigen) Ereignissen und die Messung von “Eigenzeit” (also der Dauer eines bestimmten Beteiligten, der an beiden dieser Ereignisse beteiligt war, von … bis …) sind natürlich in besonderer Weise (eher indirekt) “gekoppelt“:
das Intervall ist die größte derartige Dauer, bzgl. aller (vorstellbarer) Beteiligten, die an diesen beiden Ereignissen teilnahmen.
Was mich aber an dieser “Online-Einführung in die Spezielle Relativitätstheorie” besonders stört, ist der offenbare Versuch, die (Geometrie/Kinematik der) SR zu diskutieren, ohne die Begrifflichkeiten der (Geometrie/Kinematik der) RT im Allgemeinen erklärt zu haben, um sie konsistent benutzen zu können.
(Vielleicht sollte der Titel ja besser heißen: “Einstein bis 1915 verstehen”, oder “Minkowski verstehen”?)
Das trifft zwar sicherlich auf (zu) viele sogenannte “Einführungen in die Spezielle Relativitätstheorie” zu.
Wenigstens gibt die “Online“-(SciLogs-)Variante Gelegenheit, sich darüber öffentlich zu beklagen.
> Dass die Zeitkoordinatendifferenz bei zwei Ereignissen von Bezugssystem zu Bezugssystem variiert, ist […] bemerkenswert
Was Koordinaten betrifft (im Gegensatz zu Messwerten), sollte man eigentlich keinerlei Erwartungen hegen; und sich entsprechend auch über nichts wurdern müssen.
> […] angesichts unserer Alltagserfahrungen
> […] von unserer Alltagserfahrung entfernt
Meint das (vmtl. beides)
– entweder “Alltagserfahrung” im Sinne “selbstverständlich anwendbarer Messoperation” (insbesondere der alltäglich gewohnten Erfahrung, die Reihenfolge oder Koinzidenz seiner eigenen Beobachtungen beurteilen zu können);
– oder “Alltagserfahrung” im Sinne “bisher/meistens erlangten Messergebnissen” (z.B., dass sich manche Paare von Beteiligten schon öfter getroffen haben als andere Paare; und man erstere deshalb vorzugsweise “Enden eines Stabes” nennt und gewisse Erwartungen bzw. Vorurteile hinsichtlich der Häufigkeit weiterer Treffen dieser Beteiligten hegt)
?
(Es wäre ja schon ein Fortschritt, diese beiden Begriffe überhaupt zu unterscheiden. Geeignete/kurze verschiedene Worte, um sie entsprechend verschieden zu benennen, ließen sich gewiss finden.)
Es geht hier wohl um den Begriff der invarianten Eigenzeit (proper time) zwischen zwei Ereignissen, welch aus dem invarianten Raumzeitintervall ds² abgeleitet wird. Physikalisch entspricht das der angezeigten Zeit einer Uhr, welche bei beiden Ereignisse vor Ort war.
http://en.wikipedia.org/wiki/Proper_time
http://en.wikipedia.org/wiki/Coordinate_time
wohingegen sich die Zeitdilatation ergibt, wenn die Eigenzeit einer “bewegten” Uhr mit der Zeit synchronisierter “ruhender” Uhren verglichen wird.
Xerxes schrieb (28. Dezember 2013 12:46):
> [invariantes Intervall zwischen zwei bestimmten zueinander zeitartigen Ereignissen …]
> Es geht hier wohl um den Begriff der invarianten Eigenzeit (proper time) zwischen zwei Ereignissen
Mittelbar, ungefähr. Denn:
“Eigenzeit (proper time)” bezieht sich ja auf einen bestimmten (identifizierbaren) Beteiligten, der an beiden genannten Ereignissen teilnahm; als dessen Dauer von seiner Anzeige der Teilnahme am einen (ersten) Ereignis bis zu seiner Anzeige der Teilnahme am anderen (folgenden) Ereignis.
Und das (invariante) Intervall zwischen diesen Ereignissen ergibt sich als Maximum aller solcher Dauern; bzgl. aller (vorstellbarer) Beteiligten, die an diesen beiden Ereignissen teilnahmen.
(Falls es davon tatsächlich Ausnahmen geben sollte, denen natürlich auch eine andere, unabhängige Definition von “(zeitartigem) Interval” zugrundeliegen müsste, dann wäre solche Ausnahmen sicherlich “äußerst pathologisch” zu nennen.)
> […] aus dem invarianten Raumzeitintervall ds² abgeleitet
Was bedeutet dabei das “d“? (Betrachtung eines bestimmten Grenzübergangs?)
Und zur “Richtung des Ableitens bzw. der Herleitung”:
die Notation “²” deutet ja eher darauf hin, dass diese mathematische Operation auf etwas (Gegebenes bzw. schon Ermitteltes, also z.B. “proper time“) angewandt würde, um “das Quadrat” (bzw. “Skalarprodukt”) zu erhalten.
> Physikalisch entspricht das der angezeigten Zeit einer Uhr, welche bei beiden Ereignisse vor Ort war.
Zunächst sollte man sorgfältig zwischen den “(physischen) Anzeigen” (d.h. “Zeigerstellungen” u.Ä.) einer bestimmten Uhr einerseits und andererseits den Werten (üblicher Weise reellen Zahlen) “t” unterscheiden, die diesen Anzeigen als Koordinaten zugeordnet werden.Physikalisch lässt sich die Reihenfolge der Anzeigen ermitteln bzw. diskutieren, sowie die Dauer der betrachteten Uhr jeweils von einer bestimmten ihrer Anzeigen bis zu einer bestimmten anderen (oder zumindest: die reell-wertigen Verhältnisse solcher Dauern).
Entsprechend können die Koordinatenzahlen “t” monoton zur Reihenfolge der Anzeigen zugeordnet sein (oder eben nicht; was allerdings kaum in Betracht gezogen wird, weil ja die Reihenfolge von Anzeigen einer bestimmten Uhr als ganz selbstverständlich verstellbar gilt).
Und die Koordinatenzahlen “t” können affin (bzgl. der genannten Dauern) zugeordnet sein; oder eben nicht.
(Jedenfalls wäre erforderlich, zunächst die Dauern bzw. zumindest die reell-wertigen Verhältnisse der Dauern an sich zu messen.)
Falls die Koordinatenzahlen “t” affin (bzgl. der Dauern zwischen Anzeigenpaaren) zugeordnet wurden, nennt man die daraus resultierende Uhr übrigens “gut” (bei MTW: “good clock”); und ansonsten eben nicht.
(Und darüberhinaus ist natürlich die o.g. “Maximum”-Betrachtung wesentlich.)
> http://en.wikipedia.org/wiki/Proper_time
Von Dauer (duration) ist darin allerdings nichts zu finden (stattdessen eher leidiges Koordinaten-Geschubse).
> http://en.wikipedia.org/wiki/Coordinate_time
Dort wird zwischen “good clock” und “(any) clock” zumindest nicht ausdrücklich unterschieden …
> wohingegen sich die Zeitdilatation ergibt, wenn die Eigenzeit einer “bewegten” Uhr mit der Zeit synchronisierter “ruhender” Uhren verglichen wird.
Es ist hoffentlich kein intolerierbarer Vorgriff zu betonen, dass es (auch dabei) um den Vergleich von Dauern geht; nicht von Anzeigen (Zeiten).
@Markus Pössel
»In meinem Text ist mit Zeitintervall schlicht die Zeitkoordinatendifferenz gemeint; …«
Ja, eben. Und würde etwas dagegen sprechen, das im Text auch so formulieren?
Zeitkoordinaten kennzeichnen Mengen gleichzeitiger Ereignisse in Abhängigkeit von einem Bezugssystem S, sowie einen Abstand zwischen je zwei dieser Mengen, welcher mit einer S ruhenden Uhr zu messen ist. Es scheint doch irgendwie hervorhebenswert, dass die Zeitkoordinatendifferenz Abstände zwischen solchen Ereignismengen ausdrückt, und nicht so sehr den zwischen einzelnen Ereignissen. Und wie dann in der SR die Abstände der den Ereignissen E bzw. F jeweils entsprechenden Gleichzeitigkeitsmengen bei einem Wechsel des Bezugssystem variieren, korrespondiert mit der sog. Zeitdilatation. Der Sachverhalt scheint mir jetzt nicht sonderlich treffend dadurch umschrieben, wenn gesagt wird, es hänge vom Bezugsystem ab, welches Zeitintervall zwischen E und F vergeht.
Weil aus dem gesamten Zusammenhang – der Abschnitt heißt “Zeitintervalle”, beschreibt, wie man Zeitintervalle aus Koordinatendifferenzen berechnet, im Absatz direkt davor wird das für die analoge Aussage zur klassischen Mechanik direkt noch einmal vorgeführt – klar wird, dass Zeitkoordinatendifferenzen gemeint sind?
Und weil ich, wo irgend möglich, längere und kompliziertere Worte zugunsten einfacherer vermeiden möchte, um möglichst wenig Leser abzuschrecken? (In dieser Hinsicht ist Teil VI ohnehin schon ein ziemlich harter Brocken.)
Chrys schrieb (29. Dezember 2013 11:15):
> Abstände zwischen solchen Ereignismengen […] und nicht so sehr den zwischen einzelnen Ereignissen.
Diese beiden unterscheidbaren “Abstands“-Begriffe hängen allerdings eng zusammen.
(Wobei die “Richtung der Abhängigkeit/Herleitung/Definition/Messung” durchaus diskutabel ist.)
(Und beide können jedenfalls ohne Verwendung irgendwelcher Koordinaten ausgedrückt werden.)
> Und wie dann in der SR die Abstände der den Ereignissen E bzw. F jeweils entsprechenden Gleichzeitigkeitsmengen bei einem Wechsel des Bezugssystem variieren, korrespondiert mit der sog. Zeitdilatation.
Zunächst einmal: wenn in diesem Zusammenhang von “Gleichzeitigkeit” die Rede ist, dann wohl auch insbesondere von “Inertialsystemen”, anstatt allgemein von “Bezugssystemen“.
Das weist auch auf das wesentliche “Haar” hin, dass ich in dieser “Suppe” noch finde:
darin stecken immer noch zu viele längliche Worte, in denen sich gegenseitige Abhängigkeiten verbergen; und die deshalb dazu aufrufen, Ockhams Klinge anzulegen.
Man kann die “sog. Zeitdilatation” ja so reduzieren:
wie (in der SR, aber auch im Allgemeinen) Dauern zwischen Beteiligten verglichen werden, die nicht zueinander ruhten (aber sich wenigstens einmal trafen).
@Markus Pössel
»Weil aus dem gesamten Zusammenhang […] klar wird, dass Zeitkoordinatendifferenzen gemeint sind?«
Die Zeitkoordinatendifferenz zwischen Ereignissen E = (a,b,c,0) und F = (a,b,c,1) kann ich offensichtlich doch als das Messergebnis einer am Orte (a,b,c) ruhenden Uhr auffassen. Das legt der Text sogar nahe, und das ist ein tadelloses “Zeitintervall zwischen E und F”. Mit dieser Deutung als Messergebnis habe ich nichts falsch gemacht, doch bringt mich dann der Hinweis auf Bezugssystem und Zeitdilatation voll auf den Holzweg. Nur merke ich das als argloser Laie nicht sogleich. Einstweilen habe ich vermeintlich kapiert, dass in der SR die Ergebnisse von Zeitmessungen der Zeitdilatation unterliegen.
Ist es so abwegig, dass es auf diese Weise gelesen und verstanden wird?
OK, nur dass ich richtig verstehe: Die Sorge ist, dass jemand auf die Idee kommt, dass auch eine Zeitintervallmessung im Ruhesystem der Uhr in der SRT anders ausfällt als in der klassischen Physik?
Das sollte ich wohl in der Tat versuchen, zu entschärfen. Danke für den Hinweis.
So: Die Neufassung ist ein Kompromiss aus kurzhalten einerseits (weil Nebenbemerkung) und das potenzielle Missverständnis mit dem Ruhezeitintervall vermeiden.
Ja, so ist eine gewisse Sicherung dagegen eingebaut, versehentlich auf die falsche Zeit-Schiene zu geraten.
Im betrachteten Spezialfall der Messung mit ruhender Uhr stimmen halt Zeitkoordinatendifferenzen und Zeitmass der Uhr überein. Und vermutlich kann in einführenden Texten gar nicht genug darauf hingewiesen werden, dass letzteres auch in der SR ein von der Wahl des Bezugssystems unabhängiges Konzept von Zeit bedeutet.
Hallo Herr Pösel
Leider findet man in den populären Internetdarstellungen fast nur naive Ideen zur SRT/ART.
Mathematik-arme SRT Erklärungen laufen in die Gefahr, Pseudowissen zu erzeugen.
Diesen Fehler machen Sie nicht,
ABER
Kapitel 1,2,3,4,5,6 sind hervorragend, tragen aber leider schon den Keim eines Missverständnisses in sich.
Einmal Alltagssprache benutzt, Punkte, Raum, Zeit, Dimensionen etc. definiert und schon wird die Umkehr immer schwerer.
Die SRT und die ART sind mathematische Tools, also Werkzeuge, die bei einer begrenzten Fragestellung, akzeptable Antworten geben.
Physik ist mit seinen mathematischen Grundlagen/Prinzipia Mathematika, (auch) eine praktische Wissenschaft, GPS ohne ART misst Mist.
ABER, viele Leser machen sich nicht die Mühe, Ihnen zu folgen, weil sie einen Job suchen, sondern weil sie glauben, wenn sie Einstein verstanden haben, auch das Universum zu verstehen.
Auch EINSTEINS GEDANKENEXPERIMENTE zeigen, wo die Probleme liegen
.Fast jeder Mensch geht mit einer Selbstverständlichkeit mittels seiner Person und seinen Sinnen von einem dekohärenten dreidimesionalem Universum mit ablaufender Zeitspanne aus und alle bisher von Ihnen hier dargelegten Wege zur SRT berühren das Problem eines primär kohärenten, komplexen, nichtentitären Universums überhaupt nicht.
Ohne die Struktur komplexer Zahlen aufzuzeigen, dass alle unsere Grundannahmen von Zeit- und Raumgrößen nur in der reelen Zahlenwelt, also in unserer Entitätendekohärenz gelten, die Struktur des uns Umgebenden nur mathematisch darstellbar ist, und wahrscheinlich optimal auch nur mit Cliffordalgebra.
Ich denke, dass Sie die Leser darauf aufmerksam machen müssen, dass das Verständnis Einsteins wichtig für den Beruf eines Physikers ist, auch sehr wichtig für die Astronomie, aber im Bereich Verständnis der Struktur dessen, was uns zu dem macht, was wir sind, nur wenig beiträgt.
Sehr geehrter Herr Richthofen!
Da ich mich als Leser darauf aufmerksam gemacht fühle, dass das Verständnis Einsteins im Bereich Verständnis der Struktur dessen, was uns zu dem macht, was wir sind, nur wenig beiträgt, gestatte ich mir folgenden Einwand:
Eine unverstandene Rechnerei, mag so nützlich sein wie ein Maulesel, sie ist aber auch so unfruchtbar wie dieser. Dazu kommt, dass die Relativitätstheorie als umwälzendes philosophisches System (Reichenbach) rezipiert wurde. Das Verständnis Einsteins gehört zu den grundlegenden Fragen der Moderne. Dies für irrelevant zu erklären ist nichts anderes als eine Kapitulation vor dieser oder – im schlechtesten Fall – eine Immunisierungsstrategie gegen eine unzutreffende Theorie.
Mit freundlichen Grüßen
Peter Strohmayer
Hatte mich gefreut, dass das Projekt nicht gestorben ist und auch einen ausführlichen Kommentar
dazu geschrieben, dass in Teil vi an mehreren Stellen die Existenz einer absoluten Zeit suggeriert
wird, sowie bemerkt, dass bez. eines Bezugssystems verschiedene Ereignisse zur gleichen Zeit am gleichen Ort stattfinden können. Leider hat das nicht geklappt, offenbar weil “Kommentar abschicken” vor der extemen Rechenaufgabe steht. Mal sehn, ob es jetzt klappt.
Aha, es hat geklappt. Also, was wollte ich anmerken?
Folgende Passagen suggerieren m.E. die Existenz einer absoluten Zeit:
-“Ein Ereignis ist dabei ein Geschehen, das an einem einzigen Raumpunkt P zu einem genau
definierten Raumpunkt (soll sicher Zeitpunkt heissen) T stattfindet.”
-“… egal, wo im Raum und zu welcher Zeit sie (die Ereignisse) stattfinden…”
-“… egal wo und zu welchem Zeitpunkt das Ereignis stattfindet…”
-“”Der Ort und der Zeitpunkt, an dem Teilchen A mit Teilchen B zusammenstößt” ist, sofern
Teilchen A und Teilchen B eindeutig identifizierbar sind, auch ohne jeglichen Bezug auf
Koordinatenwerte, eine eindeutige Beschreibung eines Punktereignisses.”
M.E. sollte man von Zeit nur dann sprechen, wenn klar ist, dass sie bez. eines Bezugssystems
gemeint ist.
M.E. können auch zwei verschiedene Ereignisse bez. eines Bezugssystems zur gleichen Zeit
am gleichen Ort stattfinden (Teilchen A trifft Teilchen B, trifft Teilchen C bez. S zur gleichen
Zeit am gleichen Ort). Wichtig ist nur, dass sie das dann auch bezüglich jedes anderen
Bezugssystems tun.
Hallo Herr Dr. Pössel,
ich wollte mal nachfragen, wie es mit einem Teil 7 ausschaut ? Oder habe ich etwas übersehen ?
Bitte geben Sie doch kurz Bescheid, ob wir den Teil 7 (und evtl. weitere) noch erwarten dürfen.
Vielen Dank schon mal !
Und natürlich recht herzlichen Dank für die viele, schon bisher geleistete Mühe !!!
Liebe Grüssle aus der Schweiz
W. E.
Die nächsten Teile bis einschließlich Teil 12 sind in unterschiedlichen Stadien der Fertigstellung, und es geht auf alle Fälle weiter; allerdings hat “Einstein verstehen” in den letzten Monaten, wie so oft, dringenderen Projekten den Vortritt lassen müssen…
Markus Pössel schrieb (20. Oktober 2014 22:26):
> Die nächsten Teile bis einschließlich Teil 12 sind in unterschiedlichen Stadien der Fertigstellung, und es geht auf alle Fälle weiter [mit] “Einstein verstehen”
Man darf gespannt sein, ob in den Teilen, deren Fertigstellung absehbar ist, der (schon längst avisierte) Begriff “Lichtuhr” zur Verfügung gestellt wird;
damit, sofern jeweils ein bestimmter Beteiligter Mitglied (“Ende”) mehrerer verschiedener “Lichtuhren” sein kann, auch dessen jeweilige Beurteilungen von “Koinzidenz” (oder ansonsten: “Reihenfolge”) von Beobachtungen hier endlich diskutabel werden,
und dadurch all das an sich Unverständliche, das im Rahmen von “Einstein verstehen” bisher schon ausgebreitet wurde, entweder schließlich doch nachvollziehbar gemacht oder als entbehrlich verworfen werden könnte.
Und das wäre der Mühe sicher wert.
Am 2 Dezember 2010 hat dieses Experiment begonnen, der bisher letzte Teil ist vom 25. Dezember 2013.
Da tut sich doch eh nichts mehr, oder. Kann man endlich mal das Experiment für beendet erklären?
Sorry, aber man muss sich auch mal eingestehen können, dass man sich Event. übernommen hat!
Doch, im Hintergrund habe ich munter an den Texten bis einschließlich Teil XII weitergeschrieben; die gibt es also größtenteils schon. Zeitaufwändig ist allerdings das Erstellen der Grafiken; die sind Hauptgrund dafür, dass noch nicht mehr im Netz ist. (Zumal einige andere Projekte mit Abgabefristen “Einstein verstehen” immer mal wieder die Zeit streitig machen.) Insofern ist das Experiment alles andere als beendet, sondern geht (langsam, zugegeben) weiter. Und online kommen sicher in den nächsten Monaten auch wieder einer oder mehrere neue Beiträge.
Markus Pössel schrieb (25. Dezember 2013):
> […] kann man dreidimensionalen Raum und Zeitgerade
… Gerade?? Wohl eher: den (eindimensionalen) Zeit-Verlauf (insbesondere jedes Beteiligten in einer geeigneten, raum-füllenden “Kongruenz“) …
> zu einem vierdimensionalen Gebilde zusammenfassen, das “Raumzeit” genannt wird.
Entsprechend der beschriebenen Konstruktion spricht man allerdings genauer von “(3 + 1)-dimensionaler Raumzeit”.
> […] Die Vierdimensionalität sagt nichts anderes aus, als dass man in jedem Bezugssystem vier Angaben benötigt, um ein bestimmtes Ereignis eindeutig zu definieren: die drei Werte der Ortskoordinaten und den Wert der Zeitkoordinate.
Wohl kaum; denn Koordinatenzuordnungen mit vier bestimmten reellen Zahlen für jedes Ereignis lassen sich eins-zu-eins auf Koordinatenzuordnungen mit z.B. nur einer einzigen bestimmten reellen Zahl für jedes Ereignis abbilden;
\( \exists f : \mathbb R^4 \leftrightarrow \mathbb R \).
Die Dreidimensionalität (der “räumlichen Dimensionen”) bedeutet stattdessen ganz unabhängig von der Zuordnung irgendwelcher Koordinatenwerte, dass “räumliche Krümmung” (oder ansonsten. “Flachheit”) aus den Abstandsverhältnissen zwischen mindestens fünf geeigneten (d.h. gegenüber einander starren) Beteiligten ermittelt wird (vgl. Synges “Five point curvature detector”).
> Wenn ein Teilchen A einsam durch den Raum fliegt […] gibt es keine Unterscheidungsmerkmale, anhand derer sich ein Punkt der Bahn von den anderen unterscheiden ließe.
Immerhin könnte sich das fragliche Teilchen ja dabei mit etwas beschäftigen (z.B. in Gedanken Schäfchen zählen, oder einen SciLog-Beitrag konzipieren); und den Verlauf seiner Beschäftigung mit sich selbst dadurch unterscheidbar anzeigen.
In den Gedankenexperimenten, die Einstein uns zu verstehen gab, geht es allerdings weniger um einzelne einsame Beteiligte, sondern eher um zahlreiche unterscheidbare, die sich (i.A.) ständig beobachten können;
so dass sich der Verlauf jedes dieser Beteiligten auch dadurch zeigt, welche Anzeigen (von anderen Beteiligten) er/sie/es separat oder koinzident wahrnahm.
Das erfordert allerdings nicht, dass irgendwelche dieser Beteiligten dabei durch bestimmte “Entfernungen” voneinander charakterisiert gewesen sein müssten (also zueinander starr gewesen sein müssten).
> Um diese Bewegung zu beschreiben, sind Hilfskonstruktionen nötig, nämlich die Definition eines Bezugssystems.
Hilfskonstruktionen, bzw. Konstruktionen überhaupt, sind sicherlich nötig und möglich.
Aber es versteht sich (hoffentlich), dass das “Material” für solche eventuellen (Hilfs-)Konstruktionen ausschließlich in den Feststellungen über Koinzidenz (oder ggf. Reihenfolge bzw. Verlauf) von unterscheidbaren Wahrnehmungen der einzelnen unterscheidbaren Beteiligten bestehen kann
(und ich bin gespannt darauf, ob diese SciLogs-Serie näher darauf eingehen wird, welche Konstruktionen aus genau diesem “Material” entstehen können).
Kleine Fehlerkorrektur, im Test steht:
“Idealisierte Zeitpunkte in der Raumzeit
Als Kombination von Raum- und Zeitpunkt kann man noch eine weitere idealisierte Größe definieren, die in der Physik Punktereignis oder kurz Ereignis heißt. Ein Ereignis E ist dabei ein Geschehen, das an einem einzigen Raumpunkt P zu einem genau definierten Raumpunkt T stattfindet. Wir können symbolisch schreiben E=(P,T).”
Es muss m. E. richtig heißen:
“… zu einem genau definierten Zeitpunkt T stattfindet.”