Einstein verstehen VIII: Bezugssystemwechsel und freie Teilchen
BLOG: RELATIV EINFACH

Dies ist Teil VIII einer Online-Einführung in die Spezielle Relativitätstheorie, die hier im Blog einen “Testlauf” absolviert und später – u.a. durch Feedback der Blogleser verbessert – ein Teil des Webportals Einstein Online werden soll. Nähere Informationen zu den Hintergründen finden sich in Einstein verstehen: Ein Blogexperiment, Teil I.
[Derzeit sind online: Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7, Teil 8]
Bislang geht es in der Einleitung noch um diejenigen Konzepte aus der klassischen Physik – der Physik vor Relativitätstheorie und Quantentheorie – die man kennen muss, um zu verstehen, vor welchem Hintergrund und auf welcher Grundlage Einstein die Spezielle Relativitätstheorie einführte.
Dieser und der nächste Beitrag werden eher abstrakter sein als der Durchschnitt von “Einstein verstehen” – irgendwo in dieser Einführung muss solches Material allerdings stehen. Vermutlich werde ich zu den einleitenden Beiträgen dann noch eine zusammenfassende Kurzversion schreiben.
Im vorangehenden Teil VII hatte ich alle Möglichkeiten vorgeführt, wie man in der klassischen Mechanik von einem Bezugssystem zum anderen wechseln kann: durch Verschiebung von Raum- und Zeitnullpunkt (konstante bzw. bei den Raum-Translationen auch zeitlich veränderliche Translationen), durch Rotationen um eine feste Achse (ditto) oder, allgemeiner, durch Hintereinanderausführen dieser elementaren Operationen.
Nun sind Bezugssysteme natürlich kein Selbstzweck, sondern dienen dazu, so etwas wie Bewegung und zeitliche Veränderung in einem einheitlichen Rahmen beschreiben zu können. In diesem Teil kümmern wir uns als erstes um die Bewegung dessen, was in Teil IV von “Einstein verstehen” ein zentraler Bestandteil der Newton’schen Mechanik gewesen war, nämlich die Bewegung kräftefreier Teilchen. Solche Teilchen hatten sich dadurch ausgezeichnet, dass sie sich mit konstanter Geschwindigkeit entlang gerader Bahnen bewegen.
Konkret stellen wir uns die Frage: Unter welchen Bedingungen entspricht freie Bewegung in Bezug auf ein gegebenes Bezugssystem auch freier Bewegung in Bezug auf ein zweites? Über welche Transformationen dürfen diese Systeme zusammenhängen, damit freie Bewegung freie Bewegung bleibt, und welche Transformationen sind unter diesen Bedingungen nicht erlaubt?
Für welche Transformationen, für welche Übergänge zwischen zwei Bezugssystemen ist freie Bewegung in dem einen System auch freie Bewegung im zweiten?
Teilchenbewegungen und die Gesetze der Mechanik
In Teil IV: Klassische Mechanik – Massenpunkte, Newton’sche Gesetze, Impuls hatte ich die Newton’schen Grundgesetze der Mechanik vorgestellt. Ich hatte dabei als Annahme vorausschicken müssen, dass es mindestens ein Bezugssystem gibt, in dem die dort beschriebenen Gesetze in der angegebenen Form gelten.
Nun, wo wir uns damit beschäftigen, wie die Raum-Zeit-Beschreibungen verschiedener Bezugssysteme miteinander zusammenhängen, können wir die Frage noch konkreter fassen: Angenommen, die Newton’schen Grundgesetze gelten in einem bestimmten Bezugssystem. In welchen anderen Bezugssystemen gelten sie noch? Bei welchen der Möglichkeiten, von einem Bezugssystem in ein anderes zu wechseln, die wir in Teil VII kennengelernt hatten, behalten die Newton’schen Gesetze ihre Form bei? Die Antwort auf diese Frage wird später eine entscheidende Rolle spielen, wenn wir uns Gedanken zu der namensgebenden Relativität in Relativitätsprinzip und Relativitätstheorie machen.
Also: Bei welchen der Möglichkeiten, das Bezugssystem zu wechseln, bewegen sich Teilchen, die sich im ersten Bezugssystem mit konstanter Geschwindigkeit entlang von Raumgeraden bewegten, auch im zweiten Bezugssystem mit konstanter Geschwindigkeit entlang von Raumgeraden?
Bei genau solchen Bezugssystemwechseln nämlich gelten die Grundregeln der Newton’schen Beschreibung der Mechanik wenn im ersten, dann auch im zweiten Bezugssystem – auch wenn wir an dieser Stelle unserer Argumentation noch nichts dazu sagen können, ob auch die Formeln, welche konkrete Kräfte und ihre Wirkung beschreiben, im zweiten Bezugssystem dieselbe Form haben wie im ersten.
Affine Transformationen
Die Drehungen um konstante Winkel, Verschiebungen des Zeitnullpunkts oder des Raumnullpunkts um konstante Zeit- bzw. Raumintervalle und die speziellen Galileo-Transformationen, die wir in Teil VII betrachtet hatten, lassen sich sämtlich als Spezialfälle einer allgemeineren Transformation der Form
schreiben, mit geeignet gewählten Koeffizienten axx, axy und so weiter. Dabei hängt keiner der Koeffizienten von x, y, z oder t ab (sprich: es handelt sich in Bezug auf diese Variablen um konstante Koeffizienten). Leser, die wissen, wie man mit Vektoren und Matrizen rechnet, dürften sofort erkennen, dass sich diese Formeln mithilfe der Matrix-Multiplikation schreiben lassen als
– eine Schreibweise, die ich im folgenden nicht verwenden werde, die aber in fortgeschritteneren Texten bevorzugt wird. Sie erlaubt deutlich kürzere Formeln, als wenn man für jede der Komponenten eine getrennte Gleichung hinschreibt.
Im Vergleich mit den Formeln im Teil VII kann man direkt ablesen, welchen Werten die axx, axy, … den spezifischen klassischen Bezugssystemwechseln entsprechen, die sich auf diese Weise ausdrücken lassen. Die Verschiebung des Zeitnullpunkts um einen konstanten Wert a0 beispielsweise würde dem Spezialfall entsprechen, dass fast alle Koeffizienten in den obigen Formeln Null sind, mit Ausnahme von att = axx = ayy = azz = 1 und atc = a0. Bei der Drehung um einen konstanten Winkel Phi um die z-Achse dagegen wären die einzigen Koeffizienten, die nicht gleich Null sind, die Koeffizienten
Transformationen, die sich in der oben angegebenen Weise mit konstanten Koeffizienten schreiben lassen, heißen affine Transformationen. Sind die Koeffizienten axc, ayc, azc und atc sämtlich Null (wie z.B. bei der gerade angegebenen Rotation), spicht man von einer linearer Transformationen.
Den Beitrag der Koeffizienten axc, ayc, azc und atc können wir ganz allgemein Verschiebung oder Translation nennen, drücken diese Größen doch gerade die Verschiebungen der Raum- und Zeitnullpunkte der beiden Systeme gegeneinander aus. Anders ausgedrückt: jede affine Transformation ist eine Verknüpfung einer linearen Transformation mit einer Verschiebung.
Führt man zwei affine Transformationen hintereinander aus, um vom System S im ersten Schritt zum System S’ und in einem weiteren Schritt zum System S” zu gelangen, dann lässt sich das Ergebnis auch in der gleichen Form wie oben als eine einzige affine Transformation schreiben, die direkt von S nach S” führt. Das kann man direkt einsehen, indem man die affinen Transformationen ausschreibt; die Koordinaten x”, y”, z” und t” ergeben sich dann als affine Transformation der Koordinaten x, y, z, t. Die Rechnung ist hier bei den Hintergrundinformationen auf Seite 2 ausgeschrieben. Durch solches Hintereinanderausführen lassen sich affine Transformationen einfach kombinieren. Ganz analog lässt sich auch das Hintereinanderausführen zweier linearer Transformationen als eine einzige lineare Funktion schreiben.
Reguläre affine Transformationen
Nicht alle affinen Transformationen, also nicht alle Möglichkeiten, die Koeffizienten axx, axy, … zu wählen, entsprechen sinnvollen klassischen Koordinatentransformationen. Wir hatten in Teil VI: Was heißt es, das Bezugssystem zu wechseln? gefordert, jedes Bezugssystem müsse jedem möglichen Punktereignis eindeutige Koordinatenwerte t(E), x(E), y(E), z(E) zuordnen. Mithilfe dieser Koordinatenwerte muss sich ein solches Punktereignis eindeutig identifizieren, insbesondere also von allen anderen Punktereignissen unterscheiden lassen. Das war überhaupt die Voraussetzung dafür gewesen, dass wir Übergänge von einem Bezugssystem zum anderen in Form von Koordinatentransformationen hinschreiben konnten.
Die oben angegebene allgemeine affine Form lässt Fälle zu, in denen diese Grundregel verletzt wird. Zu den einfachsten Beispielen gehört der Fall, in dem axx=1 gilt und alle anderen Koeffizienten Null sind. Offensichtlich würden über solch eine Transformationsformel unendlich vielen verschiedenen Elementarereignissen, die sich im ersten Bezugssystem anhand ihrer y-, z- und t-Koordinatenwerte auseinanderhalten lassen, ein und derselbe Satz von Koordinatenwerten im zweiten Bezugssystem zugeordnet. Die im ersten Bezugssystem mit x=1, y=2, z=3, t=4 und x=1, y=1, z=1, t=1 beschriebenen zwei verschiedenen Elementarereignisse beispielsweise bekommen dieser Transformation gemäß im zweiten Bezugssystem beide die Koordinaten x’=1, y’=0, z’=0, t’=0 zugeordnet, sind dort also nicht unterscheidbar.
Wir müssen an die Koeffzienten daher die Forderung stellen, dass beim Übergang vom ersten ins zweite Bezugssystem die eindeutige Zuordnung von Koordinatenwerten erhalten bleiben muss. Die Koeffizienten, die diese Forderung erfüllen, entsprechen den regulären affinen Transformationen. Alternative Bezeichnungen für reguläre affine Transformationen sind nicht-singuläre oder invertierbare affine Transformationen.
Invertierbarkeit, zu deutsch: Umkehrbarkeit, drückt dabei aus, was direkt aus der Eindeutigkeitsforderung folgt, mit der wir die Koordinatentransformationen in Teil VI überhaupt erst definiert hatten: Weil die Zuordnung von Koordinatenwerten zu Elementarereignissen eindeutig ist, können wir zu jedem Satz von Koordinatenwerten im ersten Bezugssystem den entsprechenden Satz von Koordinatenwerten im zweiten Bezugssystem finden – aber (natürlich!) auch umgekehrt.
Allgemeine Galilei-Transformationen
Selbst die regulären affinen Transformationen enthalten noch viel mehr Abbildungen als nur jene besonderen Koordinatentransformationen, von denen wir in Teil VII gezeigt hatten, dass sie die einzigen in der klassischen Mechanik zulässigen Übergänge zwischen Bezugssystemen sind.
Um den Anforderungen der klassischen Mechanik zu genügen, müssen axx, axy, axz, ayx, ayy, ayz, azx, azy, azz gerade diejenige Form haben, die man erhält, wenn die beiden Bezugssysteme durch eine Drehung um einen konstanten Winkel um eine beliebige feste Achse (möglicherweise in Kombination mit einer Achsenspiegelung) zusammenhängen. (In der Matrixschreibweise entspricht das der Forderung, die durch diese Koeffizienten gebildete Teilmatrix R solle orthogonal sein, RRT = RTR = I3 mit I3 der dreidimensionalen Einheitsmatrix.)
Außerdem muss in der klassischen Mechanik atx = aty = atz =0 und att= 1 gelten. Das folgt aus der Forderung, dass Beobachter, egal von welchem Bezugssystem aus, für Zeitintervalle zwischen zwei gegebenen Ereignissen denselben Wert erhalten sollen. Daher sind für die Zeitkoordinate nur konstante Verschiebungen des Zeitnullpunkts als Transformationen zugelassen.
Die Koeffizienten axt, ayt und azt dagegen dürfen konstante Werte ungleich Null haben. Das entspricht dem Beitrag der speziellen Galilei-Transformationen, also den Transformationen zwischen zwei Bezugssystemen, deren Raumnullpunkte sich relativ zueinander mit konstanter Geschwindigkeit bewegen.
Auf diese Weise erhält man jene besonderen affinen Transformationen, die mit der klassischen Mechanik vereinbar sind. Sie heißen allgemeine Galilei-Transformationen.
Per Definition sind die allgemeinen Galilei-Transformationen eine Untermenge der regulären affinen Transformationen. Das ist aus dem folgenden Grunde praktisch: Wenn wir allgemein zeigen können, dass alle regulären affinen Transformationen eine bestimmte Anforderung erfüllen, dann ist damit automatisch gezeigt, dass auch die allgemeinen Galilei-Transformationen diese Anforderung erfüllen. Genau so werden wir weiter unten an die Frage nach den geradlinig-gleichförmigen Bahnen herangehen, nach den Bahnen freier Teilchen.
Kombinationen und Umkehrtransformationen
Eine wichtige Eigenschaft von affinen Transformationen ist, dass die Umkehrung einer regulären affinen Transformation selbst auch eine reguläre affine Transformation ist. Die Umkehrtransformation lässt sich in derselben Form mit Termen proportional zu x’,y’,z’,t’ und konstanten Termen schreiben, wie wir es oben für affine Transformationen gezeigt haben, bei denen die x, y, z, t auf der rechten Seite stehen und jeweils geeignete Konstanten vor sich stehen haben.
Der allgemeine Nachweis dieses Umstands würde uns tiefer in die lineare Algebra führen, als ich es hier vorhabe. Für die speziellen affinen Transformationen, die in der klassischen Mechanik von Wichtigkeit sind, also die allgemeinen Galilei-Transformationen, ist der Beweis günstigerweise deutlich einfacher.
Zumindest für die Translationen um einen konstanten Betrag, für die Rotationen um x-, y- und z-Achse und die speziellen Galilei-Transformationen, hatten wir nämlich jeweils bereits in Teil VII gezeigt, dass die jeweiligen Umkehr-Transformationen dieselbe Form haben wie die betreffenden Transformationen selbst. Das heißt insbesondere auch, dass die Umkehrtransformationen ihrerseits jeweils affine Transformationen sind. Anders gesagt: Wenn wir eine einzelne Translation, eine einzelne Galilei-Transformation, eine einzelne Rotation um die x-, y- oder z-Achse betrachten, dann gilt in der Tat, dass auch die Umkehrtransformation dazu eine affine Transformation ist.
Ich nennen diese einfachen Transformationen, aus denen sich alle anderen durch Hintereinanderausführen ableiten lassen, ab jetzt elementare Galilei-Transformationen (Translation um konstanten Betrag, Rotation um x-, y- oder z-Achse um konstanten Winkel oder spezielle Galilei-Transformation).
Jetzt müssen wir uns nur noch Gedanken dazu machen, wie es sich verhält, wenn wir mehrere affine Transformationen hintereinander ausführen. Bereits um allgemeine Rotationen zwischen Bezugssystemen vorzunehmen, mussten wir schließlich mehrere verschiedene Rotationen um unterschiedliche Koordinatenachsen hintereinander vornehmen. Allgemeiner ergibt jede Kombination von konstanten Translationen, x-, y- oder z-Rotationen und speziellen Galilei-Transformationen eine in der klassischen Mechanik zulässige Transformation.
Dass die Umkehrtransformationen solcher durch Hintereinanderausführen erhaltener Transformationen jeweils affine Transformationen sind, kann man am einfachsten sehen, wenn man sich klar macht, wie sich hintereinander ausgeführte Transformationen umkehren lassen. Seien A und B zwei der elementaren Galilei-Transformationen. Wir führen A und B hintereinander aus, um vom Bezugssystem S zunächst mithilfe von A zum System S’ zu kommen (also die S’-Koordinaten in Abhängigkeit von den S-Koordinaten auszudrücken). Anschließend gehen wir mithilfe der Transformation B vom System S’ zum System S” über. Symbolisch kann man diesen Übergang wie folgt schreiben:
Wie sieht die Umkehrung dieser Kombination aus? Wie kommen wir vom System S” zurück zum System S, drücken also Koordinaten x, y, z, t in Abhängigkeit von den Koordinaten x”, y”, z”, t” aus?
Indem wir Schritt für Schritt rückwärts vorgehen, freilich, wie es beim Rückwärtsgehen üblich ist, in umgekehrter Reihenfolge! Wir wissen, dass es sowohl zu A als auch zu B jeweils eine Umkehrung gibt, die ihrerseits eine affine Transformation ist. (Das wissen wir, weil A und B elementare Transformationen sind – konstante Translation, oder x-/y-/z-Rotation um konstanten Winkel, oder spezielle Galilei-Transformation. Für solche elementaren Transformationen hatten wir die Umkehrungen explizit hingeschrieben, und es waren in der Tat jeweils affine Transformationen.) Nennen wir diese Umkehrungen entsprechend einer weit verbreiteten Schreibweise A-1 (als Umkehrung von A) und B-1 (als Umkehrung von B).
Wie kommen wir von S” zurück zu S’? Indem wir die Umkehrung von B anwenden, nämlich B-1. Wie kommen wir im zweiten Schritt von S’ zurück nach S? Indem wir A-1 anwenden, nämlich die Umkehrung von A. Die Transformationen B-1 und A-1, hintereinander ausgeführt, ergeben die Umkehrung der Transformation, die uns von S nach S” geführt hat, symbolisch dargestellt so:
Zwei hintereinander ausgeführte affine Transformationen, das hatte ich bereits erwähnt (und ist auf der Hintergrundinformations-Seite explizit ausgerechnet), lassen sich immer als eine einzige affine Transformation von S” nach S schreiben. Ganz analog können wir argumentieren, wenn wir mehr als zwei affine Transformationen hintereinander ausführen und die Umkehrung der daraus resultierenden affinen Transformation suchen.
Mithilfe dieser Argumentation können wir jetzt ganz allgemein sagen: Nicht nur die allgemeinen Galilei-Transformationen sind affin, sondern auch ihre jeweiligen Umkehrungen.
Kleiner Exkurs: Mathematische Eigenschaften
In der Matrixschreibweise entspricht die Forderung, dass sich die Koordinatentransformation umkehren lässt, der Forderung, dass die Matrix M invertierbar sein möge. In der linearen Algebra, also jenem Teilgebiet der Mathematik, das sich mit linearen Abbildungen, Matrizen, Vektoren und damit zusammenhängenden Konzepten beschäftigt, lernt man, dass dies gleichwertig ist mit der Aussage, dass die Determinante der Matrix – eine charakteristische Zahl, die man jeder Matrix in Abhängigkeit von ihren Einträgen zuordnen kann – ungleich Null ist.
Wie schon angemerkt: Durch direktes Hintereinanderschreiben und Ausrechnen kann man sich davon überzeugen, dass zwei hintereinander ausgeführte affine Transformationen wiederum eine affine Transformation ergeben. Affine Transformationen lassen sich miteinander verknüpfen, und das Ergebnis ist seinerseits eine affine Transformation, mit genau der gleichen Form, sprich: genau der gleichen Kombination aus Koordinatenwerten und konstanten Koeffizienten wie oben für die x,y,z,t, die x’, y’, z’, t’ und die Koeffizienten axx, … angegeben. Dasselbe gilt, wie erwähnt, für die linearen Transformationen: zwei lineare Transformationen, hintereinander ausgeführt, lassen sich als eine einzige lineare Transformation schreiben.
Der Umstand, dass wir uns auf reguläre, also umkehrbare affine Transformationen beschränken, zusammen mit einer abstrakteren Eigenschaft namens Assoziativität (salopp gesagt: beim hintereinander Ausführen von Koordinatentransformationen kommt es nicht darauf an, für welche/s der Transformations-Paare man die Kombination zuerst ausrechnet) führt dazu, dass die allgemeinen Transformationen etwas bilden, das unter Mathematikern Gruppe heißt. Die regulären affinen Transformationen bilden untereinander eine eigene Gruppe, und die regulären linearen Transformationen ebenso.
Geradenbahnen
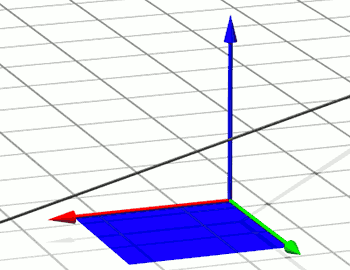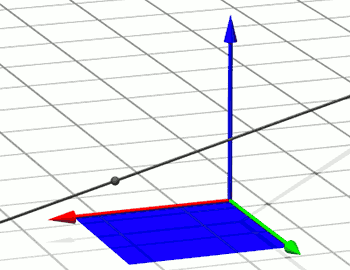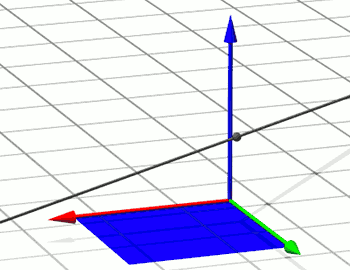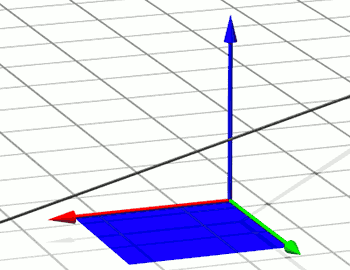
Um zu prüfen, was beim Bezugssystem-Wechsel mit Teilchen passiert, die sich mit konstanter Geschwindigkeit entlang einer Raumgeraden bewegen, sehen wir uns als erstes genauer an, wie sich solche Bahnen mithilfe von Koordinaten beschreiben lassen. Die nachfolgende Abbildung zeigt eine solche Geradenbahn. Entlang der Gerade, deren im Bild sichtbarer Abschnitt in grau eingemalt ist, legt das Teilchen jeweils in gleichen Zeitintervallen gleiche Strecken zurück:
Nun betrachten wir, wie sich der Abstand des Teilchens von der xy-Ebene mit der Zeit ändert. Dazu verbinden wir jeden Punkt der Teilchenbahn über eine geeignete Hilfsgerade, die parallel zur z-Achse ist, mit der xy-Ebene.
 Im Bild rechts ist die Ebene dargestellt, die durch die Bahngerade und diese Hilfsgeraden aufgespannt wird. Der schräge graue Geradenabschnitt ist die Teilchenbahn, die gepunkteten Linien sind zwei Beispiele für solche Hilfsgeraden, und der waagerechte blaue Geradenabschnitt unten im Bild ist die Schnittgerade der Bildebene mit der xy-Ebene.
Im Bild rechts ist die Ebene dargestellt, die durch die Bahngerade und diese Hilfsgeraden aufgespannt wird. Der schräge graue Geradenabschnitt ist die Teilchenbahn, die gepunkteten Linien sind zwei Beispiele für solche Hilfsgeraden, und der waagerechte blaue Geradenabschnitt unten im Bild ist die Schnittgerade der Bildebene mit der xy-Ebene.
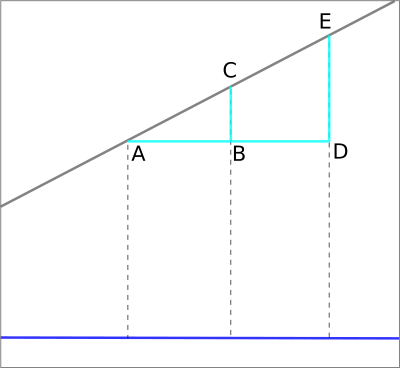
Hilfsgeraden und Geradenbahn verlaufen immer in demselben konstanten Winkel zueinander (sie liegen, wie hier dargestellt, in derselben Ebene; es geht jeweils um Geradenabschnitte; alle Hilfsgeraden sind parallel zur z-Achse und damit parallel zueinander, und bilden damit mit einer weiteren Gerade, der Bahngerade, alle denselben Winkel).
Das heißt auch: Geht man von einem gewählten Ausgangspunkt auf der Teilchenbahn weiter die Bahn entlang, dann sind die entlang der Bahngeraden zurückgelegte Strecke und das Anwachsen des Abstandes von der xy-Ebene (also der Streckenzuwachs der Hilfsgeraden) proportional zueinander, wie man entlang der eingezeichneten ähnlichen Dreiecke ABC und ADE direkt sehen kann:
Dass sich das Teilchen entlang seiner Bahn mit konstanter Geschwindigkeit bewegt, entspricht dem Zusammenhang
wobei s(t) die von einem bestimmten Referenzpunkt aus entlang der Bahn zurückgelegte Strecke ist. Wenn nun aber die Strecke proportional zur Zeit t anwächst, und der Streckenzuwachs proportional ist zum Abstand von der xy-Ebene, dann wächst auch die Länge der zur Verbindung mit der xy-Ebene benötigten Hilfsgeradenabschnitte proportional zur Zeit. Diese Länge, der kürzeste Abstand vom Teilchenort zur xy-Ebene, das hatten wir bereits in Teil I im Abschnitt kartesische Koordinaten so festgelegt, definiert den z-Koordinatenwert des Ortes des Teilchens im Raum. Die z-Komponente der Bahngleichung des Teilchens ist demnach ebenfalls linear in der Zeit,
mit vz und z0 Konstanten. vz ist das, was wir in Teil IV als z-Komponente der Teilchengeschwindigkeit eingeführt hatten, dort freilich noch ohne ausführliche geometrische Begründung, und z0 ist der z-Koordinatenwert des Teilchens zur Zeit t=0.
Ganz analog können wir auch mit Projektionen auf die xz-Ebene und auf die yz-Ebene argumentieren. Als Ergebnis erhalten wir, dass die Koordinaten-Bahngleichungen für ein Teilchen, das sich mit konstanter Geschwindigkeit entlang einer Raumgeraden bewegt, die folgende Form besitzen:
Dabei sind die vx, vy, vz und x0, y0, z0 Konstanten (hängen also weder von x,y,z noch von t ab).
Geradenbahnen und affine Koordinatentransformationen
Angenommen, ein Teilchen folgt in einem bestimmten Bezugssystem einer Geradenbahn, beschrieben durch drei lineare Gleichungen wie die gerade genannten. Welche Bahn hat es dann in einem zweiten Bezugssystem, das über eine affine Koordinatentransformation mit dem ersten zusammenhängt?
Wir schränken uns dabei absichtlich nicht auf die spezielle Form der Galilei-Transformationen ein. Eine Zusatzannahme müssen wir allerdings doch machen, nämlich, dass unsere (affinen, regulären) Transformationen überhaupt Teilchenbahnen in Teilchenbahnen überführen. Rein mathematisch gesehen kann eine lineare Transformation eine gerade Teilchenbahn (jedem Zeitpunkt ist der aktuelle Ort des Teilchens) auch in eine Raumgerade überführen, die nur zu einem einzigen Zeitpunkt t’ existiert. Das wollen wir ausschließen und uns auf Transformationen beschränken, in denen auch der Beobachter im zweiten Bezugssystem ein Teilchen sieht, das sich mit der Zeit fortbewegt, sprich: dem sich für jeden Zeitkoordinatenwert t’ in einem Zeitintervall, das nicht nur aus einem einzelnen Zeitpunkt besteht, ein Ort zuordnen lässt. Ich nenne die affinen Transformationen, die diese Bedingung erfüllen, bahnerhaltend.
Was ist unter diesen Umständen die Bahn des entsprechenden Teilchens, ausgedrückt im Bezugssystem S’, das mit S durch eine affine Transformation der oben genannten Form verbunden ist? Dazu nutzen wir die oben angegebenen Transformationsgleichungen von x,y,z,t nach x’, y’, z’, t’, in denen nur die Koeffizienten axx, … vorkommen.
Zuerst setzen wir die Bahngleichung des Teilchens in die Transformationsgleichung für t’ ein, also in die Gleichung
um in dieser Gleichung x, y, z jeweils durch t und die Koeffizienten vx, vy, vz und x0, y0, z0 zu ersetzen. Das Ergebnis ist
Wäre der Ausdruck in der Klammer vor dem t gleich Null, dann hätten wir es gerade mit dem erwähnten Fall einer Raumgeraden zu tun, die nur bei einem einzigen konstanten Wert für t’ definiert ist. Diesen Fall hatten wir ausdrücklich ausgeschlossen und im Gegenteil angenommen, dass das Teilchen auch aus Sicht des Bezugssystems S’ eine Bahn entlangläuft, sich also für jeden Zeitkoordinatenwert t’ in dem von uns bestrachteten Zeitintervall an einem bestimmten Ort befindet. Das geht nur, wenn der Ausdruck in den runden Klammern ungleich Null ist. Dann aber können wir die Gleichung direkt auflösen und erhalten entlang der Bahn des Teilchens die Beziehung
zwischen den Zeitkoordinatenwerten t und t’.
Setzen wir diese Beziehung in die Bahngleichungen x(t), y(t) und z(t) ein, und diese wiederum in die affinen Transformationsgleichungen für das gestrichene System S’, dann erhalten wir für das betrachtete Teilchen im System S’ eine x’-Bahngleichung
mit
und
Bahngleichungen für y'(t’) und z'(t’) erhalten wir ganz analog.
Das sind wiederum Geradengleichungen. Damit haben wir für bahnerhaltende, affine Transformationen ganz allgemein abgeleitet: Hängen zwei Bezugssysteme S und S’ über eine affine Transformation zusammen, dann git: Teilchen, die sich im Bezugssystem S mit konstanter Geschwindigkeit entlang gerader Bahnen bewegen, bewegen sich auch im Bezugssystem S’ mit konstanter Geschwindigkeit entlang gerader Bahnen.
Geradenbahnen, Newton’sche Mechanik und Bezugssysteme
Dass geradlinig-gleichförmige Bewegung im System S auch einer geradlinig-gleichförmigen Bewegung im System S’ entspricht, welches mit S über eine bahnerhaltende affine Transformation verbunden ist, gilt insbesondere für diejenigen Spezialfälle affiner Transformationen, die wir als Transformationen zwischen Bezugssystemen der klassischen Mechanik kennengelernt hatten: Die allgemeinen Galilei-Transformationen als Obermenge der konstanten Zeit- und Raumtranslationen, der speziellenGalilei-Transformationen und der Rotationen um einen konstanten Winkel, sowie all derer mögliche Kombinationen. Alle allgemeinen Galilei-Transformationen sind nicht nur regulär affin, sondern auch bahnerhaltend – das folgt direkt aus der Aussage, dass in der klassischen Mechanik att=1 und atx = aty = atz = 0 gilt, also t’ = t.
Nun ist, wie wir gesehen haben, auch jede Umkehrung einer allgemeinen Galilei-Transformation eine (reguläre) affine Transformation, und aufgrund von t’=t automatisch auch bahnerhaltend. Damit gilt nicht nur, dass jede geradlinig-gleichförmige Bewegung im System S einer geradlinig-gleichförmigen Bewegung im System S’ entspricht, welches mit S durch eine allgemeine Galilei-Transformation verknüpft ist. Auch umgekehrt entspricht jeder geradlinig-gleichförmigen Bewegung in S’ eine geradlinig-gleichförmige Bewegung in S.
Anders formuliert heißt das: Gilt in einem bestimmten Bezugssystem die Newton’sche Aufteilung, nach der sich eine bestimmte Klasse von Teilchen (“freie Teilchen” bzw. “kräftefreie Teilchen”) mit konstanter Geschwindigkeit entlang von Geraden bewegt, während Teilchen, die nicht zu dieser Klasse gehören durch auf sie wirkende Kräfte von solchen freien Bahnen abgelenkt werden, dann gilt genau dieselbe Unterteilung in kräftefreie und kraft-beeinflusste Teilchen auch in jedem Bezugssystem, welches mit dem erstgenannten Bezugssystem durch eine bahnerhaltende affine Koordinatentransformation zusammenhängt. Ein Teilchen, das im ersten Bezugssystem einer freien Bahn folgt, tut dies auch im zweiten System, und umgekehrt.
Der Beweis lässt sich auch in die Gegenrichtung führen. Tatsächlich gilt: Eine Koordinatentransformation, die jede mit konstanter Geschwindigkeit durchlaufende Geradenbahn in eine mit konstanter Geschwindigkeit durchlaufende Geradenbahn überführt und dabei, das muss man zusätzlich annehmen, keine Punkte “ins Unendliche verschiebt” (Raum- und Zeitpunkte mit endlichen Koordinatenwerten haben auch im zweiten Bezugssystem endliche Koordinatenwerte), ist zwangsläufig eine affine Koordinatentransformation. Dieses mathematische Ergebnis motiviert später die lineare Form der in der Speziellen Relativitätstheorie gültigen Koordinatentransformationen. Diese Beweisrichtung ist freilich ungleich anspruchsvoller und benötigt zahlreiche mathematische Werkzeuge, deren Kenntnis ich hier nicht voraussetzen kann.
Wir wenden uns stattdessen im nächsten Teil denjenigen Koordinatentransformationen der klassischen Physik aus Teil VII zu, die gerade nicht affin sind: beschleunigten Verschiebungen des Raumnullpunktes und zeitabhängigen Drehungen der Koordinatenachsen, wiederum mit der Frage: Was bedeuten die entsprechenden Bezugssystemwechsel für die Bahnen freier Teilchen?
Soweit der Entwurf des achten Teiltextes. Wie für die vorangehenden Teile von “Einstein verstehen” gilt auch für diesen hier, dass ich Veränderungen, die sich aus der hier geführten Diskussion ergeben, direkt umsetzen werde. Wenn es Änderungen gibt, stelle ich die Originalfassung hier als PDF ein. Die Zusatz-Textteile, in denen einige der Erklärungen aus dem Haupttext näher ausgeführt werden, befinden sich auf Seite 2 dieses Blogbeitrags.
Meinen Umgang mit Kommentaren in diesem Blog habe ich in diesem Blogbeitrag erläutert. Inbesondere gilt: Der obige Text stellt den achten Schritt einer systematischen Einführung in die Spezielle Relativitätstheorie dar. Die Diskussion sollte auf den hier behandelten Themenbereich beschränken und insbesondere nicht auf das vorgreifen, was erst in den nachfolgenden Teilen der Einführung angesprochen wird. Ich behalte mir vor, Diskussionsbeiträge, die dem Leser keinen Mehrwert bieten, sondern die Diskussion stören, zu löschen.
Die Kommentare können zwischenzeitlich moderiert sein und werden dann von mir jeweils erst freigeschaltet. Daher bitte Geduld, wenn Sie einen Kommentar eingestellt haben, dieser aber nicht gleich unten auf dieser Seite erscheint!


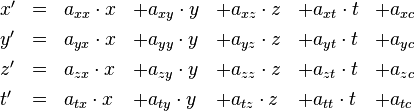
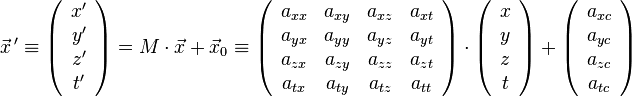
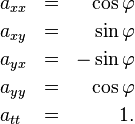
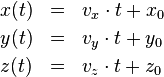
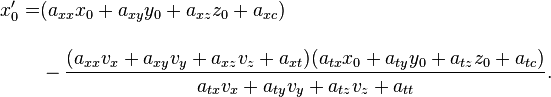
1) Da sind offenbar einige Hyperlinks verunglückt; etwas von der Form “http://http://http://http://http://https://scilogs.spektrum.de/relativ-einfach/einstein-verstehen-vii-bezugssystemwechsel-in-der-klassischen-mechanik/” kann nicht funktionieren.
2) »Wir wenden uns stattdessen im nächsten Teil denjenigen Koordinatentransformationen der klassischen Physik aus Teil VII zu, die gerade nicht affin sind: beschleunigten Verschiebungen des Raumnullpunktes und zeitabhängigen Drehungen der Koordinatenachsen, wiederum mit der Frage: Was bedeuten die entsprechenden Bezugssystemwechsel für die Bahnen freier Teilchen?«
Mit welcher didaktischen Motivation? Solche Transformationen genügen nicht dem speziellen Relativitätsprinzip und gehören nicht zur SR. In seinem populären Büchlein von 1916 hat Einstein aus guten Gründen dergleichen schliesslich auch nicht bei der SR abgehandelt.
Hyperlinks: Da spinnt das Content Management System der Scilogs gerade herum, sorry. Die zuständigen Kollegen suchen gerade nach dem Fehler; ist hoffentlich bald wieder OK.
Beschleunigungen: So etwas braucht man, um Trägheitskräfte einzuführen. Die wiederum sind sinnvoll, um Inertialsysteme zu definieren (alternativ von “kräftefreien Teilchen” zu reden ist nicht ganz urnproblematisch, siehe den Übergang zur ART). Mir ist aber bewusst, dass die Grundlage , die ich gerade entwickle, vergleichsweise tief gehen. Wie kurz angedeutet: In der Endversion von “Einstein verstehen” habe ich stattdessen vor, eine Zusammenfassung der bisherigen Vorbereitungsteile an den Anfang zu stellen. Nur wer es genauer wissen möchte, wem das Vorwissen fehlt oder wer bzw. entsprechende Missverständnisse aufklären muss, dürfte dann noch eine Ebene tiefer gehen.
…so, jetzt sollten alle Hyperlinks wieder richtig sein!
MP: “Anders formuliert heißt das: Gilt in einem bestimmten Bezugssystem die Newton’sche Aufteilung, nach der sich eine bestimmte Klasse von Teilchen (“freie Teilchen” bzw. “kräftefreie Teilchen”) mit konstanter Geschwindigkeit entlang von Geraden bewegt, während Teilchen, die nicht zu dieser Klasse gehören durch auf sie wirkende Kräfte von solchen freien Bahnen abgelenkt werden, dann gilt genau dieselbe Unterteilung in kräftefreie und kraft-beeinflusste Teilchen auch in jedem Bezugssystem, welches mit dem erstgenannten Bezugssystem durch eine bahnerhaltende affine Koordinatentransformation zusammenhängt. Ein Teilchen, das im ersten Bezugssystem einer freien Bahn folgt, tut dies auch im zweiten System, und umgekehrt.”
Gilt das auch für Photonen?
Bislang ist hier von Photonen noch nicht die Rede, und um quantenmechanische Komplikationen wird es in dieser Einführung auch nicht gehen, aber prinzipiell: Ja, wenn Lichtteilchen in einem der Bezugssysteme mit konstanter Geschwindigkeit Geradenbahnen folgen, gilt das dem hier dargelegten nach auch in anderen Bezugssystemen, die man über affine Transformationen erreicht.
Hallo Dr. Pössel,
eigentlich könnte Teil IX kommen.
mit freundlichem Gruß
Markus Pössel schrieb (16. Januar 2016):
> Tatsächlich gilt: Eine Koordinatentransformation, die jede mit konstanter Geschwindigkeit durchlaufende Geradenbahn in eine mit konstanter Geschwindigkeit durchlaufende Geradenbahn überführt und dabei, das muss man zusätzlich annehmen, keine Punkte “ins Unendliche verschiebt” (Raum- und Zeitpunkte mit endlichen Koordinatenwerten haben auch im zweiten Bezugssystem endliche Koordinatenwerte), ist zwangsläufig eine affine Koordinatentransformation.
Stattdessen gilt: Eine Koordinatentransformation, die jede mit konstanter Koordinaten-Geschwindigkeit durchlaufende Koordinaten-gerade Bahn in eine mit konstanter Koordinaten-Geschwindigkeit durchlaufende Koordinaten-gerade Bahn überführt und dabei keine Punkte “ins Unendliche verschiebt”, ist zwangsläufig eine affine Koordinatentransformation.
Die Begriffe “Geschwindigkeit (eines bestimmten Beteiligten bzgl. Mitgliedern eines Inertialsystems)” und “Bahnform (einer geeigneten Teilmenge von Mitgliedern eines Inertialsystems)” sind dagegen Koordinaten-frei definiert und feststellbar. Sie bestehen unveränderlich für jegliche Eins-zu-Eins-Zuordnung von Koordinaten-Tupeln.
Die Transformations-Beziehungen zwischen irgendwelchen zwei Eins-zu-Eins-Zuordnung von Koordinaten-Tupeln sind allerdings wesentlich allgemeiner als (nur) affine Koordinatentransformationen.
p.s.
SciLogs-Kommentar-\(\LaTeX\)-Test:
“\( s^2 : \mathcal E \times \mathcal E \rightarrow \mathbb R. \)” wird dargestellt als “\( s^2 : \mathcal E \times \mathcal E \rightarrow \mathbb R.\)”
@Frank Wappler: In den vorangehenden Teilen ist die Geschwindigkeit ja über (physikalisch sinnvolle, also nicht beliebige) Koordinaten definiert worden. Insofern: Was ich da schrieb ist so, wie ich die Begriffe eingeführt habe, richtig.
Ihr (wiederholtes) Vorgehen, Ihren eigenen Sprachgebrauch zum einzig Wahren zu erklären und alles, was davon abweicht (wie in diesem Falle) für “falsch” zu erklären, ist irreführend und letztlich auch schlampig, da es wichtige Informationen zum Kontext (wie sind die Begriffe in dieser Artikelserie definiert) unter den Tisch fallen lässt. Warum dieser Mangel an Flexibilität? Sie müssen doch selbst merken, dass das die Kommunikation noch weiter erschwert.
Markus Pössel schrieb (3. Juli 2018 @ 22:59):
> In den vorangehenden Teilen ist die Geschwindigkeit ja über […] Koordinaten definiert worden.
Das derart Definierte ist folglich als Koordinaten-Geschwindigkeit zu bezeichnen.
> (physikalisch sinnvolle, also nicht beliebige) Koordinaten
Wird es nach Jahren des Hinhaltens denn nicht endlich mal zu einer nachvollziehbaren Definition kommen, welche Koordinaten-Zuordnungen “physikalisch sinnvollen Koordinaten” genannt werden sollen ??
Dass jeweils “Eindeutigkeit” (“jedem möglichen Punktereignis eindeutige Koordinatenwerte“) bzw. Invertierbarkeit der Zuordnung gefordert ist, dürfte ja selbstverständlich und unkontrovers sein.
Aber was darüberhinaus noch ?!?
Meine naive Vermutung in Anlehnung an die vorliegenden Teile der Online-Einführung wäre ja, dass eine Koordinaten-Zuordnung \[ \frac c : \mathcal E \times \mathcal E \rightarrow \mathbb R^n \] genau dann “physikalisch sinnvoll” genannt werden soll,
falls sich eine Funktion \[ f_{\frac c} : \mathbb R^n \times \mathbb R^n \rightarrow \mathbb R \] angeben ließe,
so dass für je zwei Elemente \(A\) und \(B in \mathcal E\) gilt:
\[ f_{\frac c}[ \, \frac c[ \, A \, ] \, \frac c[ \, B \, ] \, ] \mapsto d[ \, A, \, B ] \],
wobei \[ d : \mathcal E \times \mathcal E \rightarrow \mathbb R \] ein bestimmtes, nachvollziehbares, physikalisch sinnvolles, vorab Koordinatenfrei definiertes Abstandsmaß bezeichnet.
Allerdings träfe das ganz ausdrücklich auf jede beliebige invertierbare Koordinaten-Zuordnung \(\frac c \) und jedes Abstandsmaß \(d\) zu, denn die entsprechende Funktion \( f_{\frac c} \) ließe sich ja unmittelbar durch
\[ f_{\frac c}[ \, a, \, b \, ] \mapsto d[ \frac c^{-1}[ \, a \, ], \frac c^{-1}[ \, b \, ] \, ] \]
angeben.
p.s.
Mit der mir eigenen Schlampigkeit und Unflexibilität verlasse ich mich zunächst darauf, dass \(\LaTeX\)-Formatierung von Kommentaren baldigst auch auf dieser SciLogs-Seite unterstützt wird …
@Frank Wappler: Nö, es ist völlig legitim, das Ergebnis nur “Geschwindigkeit” zu nennen. Genau dieser inflexible Ansatz, den Sie da in punkto Begriffe verfolgen, macht die Kommunikation so schwierig und eine Reihe Ihrer Äußerungen so irreführend. Sprache ist flexibel. Und für die meisten hier Mitlesenden schränkt steife Anwendung von Fachbegriffen die Verständlichkeit ein, während jeder Rückgriff auf Alltagsbegriffe hilft.
Zu “Jahren des Hinhaltens” – Ihre Anspruchshaltung ist schon ziemlich dreist. Wie schon mehrfach geschrieben: Dieses Blog läuft für mich “nebenbei”. Ich schreibe Beiträge, wenn ich neben meinen anderen Tätigkeiten Zeit dafür finde, und dann als Mischung dessen, was gerade aktuell ist, was mich gerade selbst beschäftigt, was an Grundlagen ich interessant finde etc.
Dass Sie hier (jetzt ja schon wiederholt!) mit einem Ton ankommen, als hätten Sie etwas bei mir mit bindendem Vertrag bestellt, bezahlt, und ich hätte dann nicht geliefert, ist einfach komplett daneben. Und hebt meine Motivation ganz sicherlich nicht, was einen Blogbeitrag über Koordinaten angeht.
Markus Pössel schrieb (4. Juli 2018 @ 11:46):
> Wie schon mehrfach geschrieben: Dieses Blog läuft für mich “nebenbei”. Ich schreibe Beiträge, wenn ich neben meinen anderen Tätigkeiten
Da dieser SciLog offenbar die einzige Form Barriere-freier Beziehung des MPIA mit der Offentlichkeit darstellt, definiert sich dadurch, wie engagiert und verantwortungsvoll das MPIA Barriere-freie Beziehungen mit der Offentlichkeit pflegt.
> was einen Blogbeitrag über Koordinaten angeht.
Einen SciLogs-Beitrag über Koordinaten kann man sich meinetwegen gern sparen; schließlich geht es dabei lediglich um (sprichwörtlich) “x-bliebige” eins-zu-eins-(invertierbare)-Zuordnungen” von Ereignissen bzw. Beteiligten und deren individuellen Anzeigen zu reell-wertigen n-Tupeln.
Der 24. September 2016 @ 10:56 in Aussicht gestellte “gesonderte [SciL]ogbeitrag zur Frage von Koordinaten und koordinatenfreien Darstellungen“ ist (für mich) vielmehr hinsichtlich der dabei angedeutenten “koordinatenfreien Darstellungen” von Interesse (die nachträglich in die Menge reell-wertiger n-Tupel und durch deren “natürliche” topologische bzw. metrische Eigenschaften abgebildet werden mögen).
p.s.
SciLogs-Kommentar-HTML-Test:
“𝔠<sup>-1</sup>” wird dargestellt als: “𝔠;-1″.
@Frank Wappler: Hoppla, da jagt ja eine falsche Aussage die nächste…
Dieses SciLog ist kein Angebot des MPIA, sondern ein Blog, das ich als einzelner Wissenschaftler, wenn natürlich auch mit engem Bezug zu meiner Arbeit am Haus der Astronomie bzw. am MPIA, schreibe. Die MPIA-Öffentlichkeitsarbeit sieht vom Tag der Offenen Tür und öffentlichen Vorträgen an diversen Orten über Pressemitteilungen und die direkte Beantwortung von Anfragen ganz anders aus.
Bei den Koordinaten sieht es mir nach dem, was Sie schreiben, doch noch aus, als wäre auch für Sie ein entsprechender Beitrag wichtig. Physiker verknüpfen ihre Koordinaten ja ganz absichtlich mit physikalischen Größen, so dass das Ergebnis keine beliebige Zuordnung hat, sondern möglichst dicht an der Physik ist. Daher sind hier beim Thema Gleichzeitigkeit ja auch die Ausführungen zur in den üblichen Standardkoordinaten dargestellten Lorentz-Transformationen hilfreich. Gerade weil es nicht um willkürliche Zahlenwerte geht sondern um physikalische Bezüge.
P.S.: Ich weiß gar nicht, ob man die SciLogs tatsächlich als barrierefrei einstufen kann; wer z.B. nur eingeschränkt sehen kann, bräuchte ja trotzdem zusätzliche Hilfsmittel, um an die Inhalte zu kommen.
Markus Pössel schrieb (5. Juli 2018 @ 12:48):
> Dieses SciLog ist kein Angebot des MPIA
Das ist nicht zu bestreiten.
In Ermanglung eines SciLogs (oder eines vergleichbar öffentlichem, archivierten und Barriere-freien Mediums), das vom MPIA ausdrücklich angeboten würde, bleibt dieses SciLog allerdings (meiner bisherigen Kenntnis nach) das dahingehend auffindbarste.
> Die MPIA-Öffentlichkeitsarbeit […] die direkte Beantwortung von Anfragen
Bietet das MPIA etwa an, Anfragen öffentlich und archiviert (d.h. mit URL versehen, wie wir es von den SciLogs her kennen und ggf. nutzen) zu stellen ??
> Physiker verknüpfen ihre Koordinaten ja ganz absichtlich mit physikalischen Größen […]
Von der in Aussicht stehenden Darstellung und Diskussion, wer welche Absichten durch das eine oder andere Anknüpfen von Koordinaten verfolgt und ggf. verwirklicht werden mögen, verspreche ich mir jedenfalls, dass die Rolle der physikalischen Größen bzw. ihrer jeweiligen Werte dadurch gewürdigt und betont wird, und dass sich alles Anschließende darauf konzentrieren kann.
> P.S.: Ich weiß gar nicht, ob man die SciLogs tatsächlich als barrierefrei einstufen kann; wer z.B. nur eingeschränkt sehen kann, bräuchte ja trotzdem zusätzliche Hilfsmittel, um an die Inhalte zu kommen.
Wer bestimmte Hilfs
modellemittel benennen kann, hat allein dadurch schon eine Barriere weniger …@Fred Wappler: Das ist eine so krude Mischung aus Unlogik, Ablenkung und dem Kapern eines bereits definierten Begriffs (Barrierefreiheit) dass ich mir eine längere Antwort erspare. Auf diese Weise kann man nicht vernünftig diskutieren.