Kosmische Expansion: Der Skalenfaktor
BLOG: RELATIV EINFACH

Ich habe gerade meine Vorlesungsunterlagen zur Kosmologie überarbeitet; gestern war ich damit bei unserem Astronomiekurs für Lehramtsstudierende wieder an der Reihe. Ich hatte letztes Jahr Gelegenheit – bei der Vorbereitung des letzten solchen Kurses, aber auch bei einer Blockvorlesung für Mastersstudenten und Doktoranden und einer Sommerschule für Lehrer – mich vertieft mit der Frage auseinanderzusetzen, was es eigentlich heißt (und was nicht), dass das Universum expandiert. Insbesondere habe ich dabei viel darüber gelernt, wo man bei diesem Thema überall in (u.a. mit Veranschaulichungen) die Irre tappen kann.
Dazu zukünftigen Beiträgen mehr; wie bei anderen Themen (Raum, Zeit, Wahrscheinlichkeit…) gilt: Am wenigsten problematisch ist es bei der kosmischen Expansion, sie in mathematische Begriffe zu fassen. Der grundlegende und einfachste Begriff heißt kosmischer Skalenfaktor; um den soll es in diesem Beitrag hier gehen.
Wir arbeiten uns dafür wieder entlang einfacher Modelle vor. Unsere erste Vereinfachung ist, dass wir als Elementarbausteine des räumlichen Aufbaus unseres Universums Galaxien nehmen. Was in diesen Galaxien im Einzelnen vorgeht – mit den Millionen oder gar Milliarden von Sternen und Planeten oder was da sonst noch an Materieformen herumschwirrt – vernachlässigen wir.
Betrachten wir zuerst ein statisches Universum. Jede Galaxie sitzt dabei irgendwo im Raum an ihrem Platz. Wir können all diese Galaxien durchnummerieren, wie hier anhand eines kleinen Ausschnitts angedeutet:
Die Galaxienbildchen sind dabei im Vergleich zu den Abständen sehr groß eingezeichnet; in Wirklichkeit wären sie kleiner.
Bezeichnen wir die Entfernung zwischen der Galaxie Nr. 1 und der Galaxie Nr. 2 mit d12, wie hier eingezeichnet: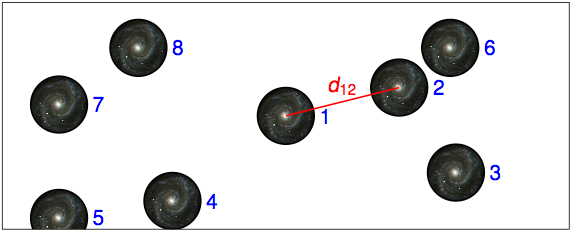
Bezeichnen wir allgemeiner, die Entfernung zwischen der Galaxie mit der Nummer i und jener mit der Nummer j als dij, dann beschreiben all diese Abstände dij vollständig, wie die Galaxien in unserem Modellkosmos angeordnet sind.
Soweit, so gut.
Als nächste Verallgemeinerung können wir annehmen, dass die Abstände dij sich mit der Zeit ändern – dass es sich also nicht um Konstanten handelt, sondern um Funktionen dij(t), die von der Zeit abhängen. Auf diese Weise könnten wir jetzt jede beliebige Bewegung der Galaxien durch- und umeinander beschreiben.
Die kosmische Expansion ist ein einfacher Spezialfall der Abstandsänderung: jener in dem sich alle Abstände auf die gleiche Art und Weise, nämlich proportional zu einem universellen kosmischen Skalenfaktor a(t) mit der Zeit ändern. All diese Abstände ändern sich wie
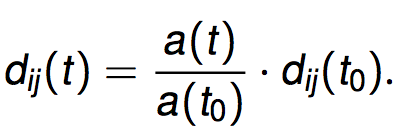
Und der einzige zeitabhängige Faktor darin ist für alle dij derselbe, nämlich a(t).
Wächst a(t) mit der Zeit, dann wachsen die Abstände aller Galaxien untereinander mit der Zeit. Das ist es, was in den heutigen kosmologischen Modellen mit kosmischer Expansion gemeint ist: Wachstum aller gegenseitigen Galaxienabstände mit der Zeit, proportional zu demselben Faktor (eben dem kosmischen Skalenfaktor).
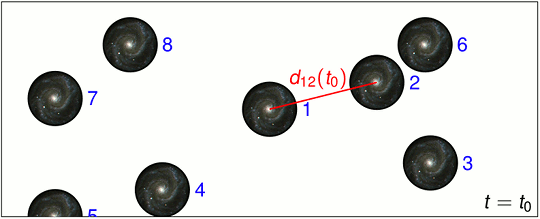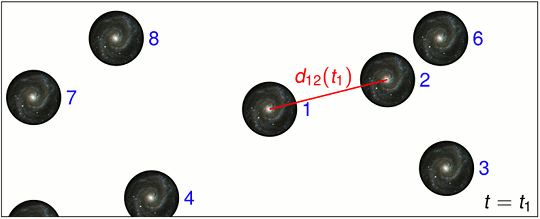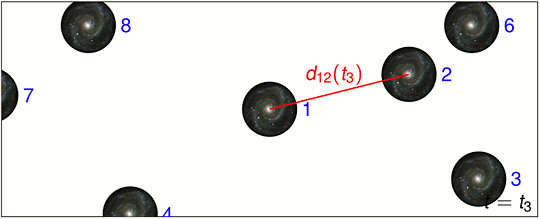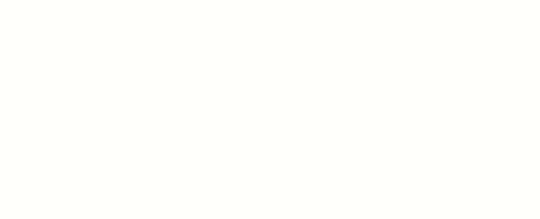
So etwas also, wie hier mit einigen Momentaufnahmen angedeutet ist:
Das Muster bleibt erhalten, und alle Abstände nehmen in gleicher Weise zu.
Einige Eigenschaften der Skalenfaktor-Expansion
In der obigen Abbildung ist die Galaxie 1 immer am gleichen Ort dargestellt. Das ist freilich eine völlig willkürliche Auswahl. Um die allgemeine Zunahme der Entfernungen zu verbildlichen, kann man genau so gut jede andere Galaxie in den Mittelpunkt stellen und dort festhalten.
Ebenso gilt: Eine Beobachterin z.B. auf der Galaxie 1 sieht, wie sich alle anderen Galaxien von ihr entfernen. Das berechtigt die Beobachterin aber nicht, für ihre Galaxie eine Sonderstellung zu beanspruchen (“Alle fliegen von uns weg; unsere Galaxie muss besonders unattraktiv sein!”). Bei der hier beschriebenen Entfernungszunahme-mit-Skalenfaktor macht jeder Beobachter und jede Beobachterin dieselbe Beobachtung, egal auf welcher Galaxie er/sie zuhause ist.
Was die Art und Weise angeht, wie sich das Universum ausdehnt, sind daher alle Galaxien gleichberechtigt.
Bei “Expansion” denken viele zuerst an eine Zunahme des Volumens – der Luftballon, den man aufpustet; die Wasserbombe, die, am Wasserhahn hängend, anschwillt. Zunächst einmal sollte aus der Beschreibung hier klar geworden sein, dass die Sichtweise bei der kosmischen eine andere ist. Was zunimmt, sind die Abstände zwischen den Modellgalaxien. Dabei ist, sicher, nachher mehr Raum zwischen diesen Galaxien als vorher – in diesem Sinne nehmen Raumbereiche, deren Grenzen wir über Galaxien definieren (z.B. Würfel mit einer Galaxie an jeder Ecke) tatsächlich an Volumen zu und expandieren. Aber davon, dass das Universum als Ganzes hier an Volumen gewönne, ist in diesem Bild zunächst einmal nicht die Rede. Die Definition der Skalenfaktor-Ausdehnung lässt sich auch in jedem Teilbereich unseres Modelluniversums wiederfinden. In der Tat sind einige der einfachsten kosmologischen Modelluniversen von vornherein unendlich groß. In diesem Falle sind das Gesamtvolumen und seine etwaige Vergrößerung gar nicht vernünftig definiert. Von kosmische Expansion kann man aber auch in solch einem unendlich großen Universum sinnvoll sprechen, denn, wie schon mehrfach gesagt: Expansion soll hier ja nur bedeuten, dass sich die Abstände zwischen den Modellgalaxien alle proportional zu ein und demselben Skalenfaktor a(t) vergrößern.
Und da haben wir sie, die Grundlage für alle Diskussionen über die kosmische Expansion: Die Beschreibung von Abstandsänderungen mithilfe eines universellen Skalenfaktors a(t). Welche anschaulichen Vorstellungen man über die kosmische Expansion auch entwickeln mag: man sollte sie, wo immer möglich, mit dieser Definition vergleichen. Wo die beiden nicht zusammenpassen, da findet die betreffende anschauliche Vorstellung offenbar ihre Grenzen.



Ich habe da mal ne Laienfrage.
Giebt es Galaxieen am Rand? also welche bei denen ich wenn unsere Erde dort währe z.B. nur auf der Nordhalbkugel Sterne sehe und auf der Südhalbkugel einen leeren Raum. Und wenn nicht, warum giebt es solche Galaxieen nicht?
Nach allem, was wir wissen, sind de Galaxien gleichmässig im Raum verteilt. Damit gäbe es keinen “Rand des Universums”, hinter dem man einfach keine Galaxien antrifft.
Zumindest in dem Teil des Universums, den wir überblicken können, scheint das so zu sein.
Ob das heißt, dass das Universum immer so weiter geht – und damit unendlich groß ist, und überall mit Galaxien gefüllt – oder ob das Universum sozusagen in sich zurück gebogen ist (sprich: wenn man lange genug in eine Richtung flöge, käme man irgendwann an den Ausgangsort zurück – lässt sich nicht entscheiden.
Danke für die Antwort. Ich merke wie sich mein Geist krümmt weil er es nicht fassen kann 🙂
Der Grundgedanke aus dem meine Frage kommt ist die Urknalltheorie. Wenn alles aus einem Punkt kommt uns sich ausdehnt dann müsste es doch ein aussen geben.
Wenn ich einen Felsen im Weltalt sprenge dann giebt es Teil die nach einer definierten Zeit am weitesten entfernt sind vom Ursprung der Explosion. Und “vor” diesen Teilen ist nichts, alle anderen Stücke kommen danach, sie sind also am Rand der ausbreitungswelle. Oder ist das mit der Urknalltheorie nicht vergleichbar?
Nein, das ist ein missverständliches Bild der Urknalltheorie. Zu erklären, wie man das besser verstehen kann hatte ich mir auf alle Fälle für einen zukünftigen Blogbeitrag vorgenommen.
Danke! Da freue ich mich schon drauf.
Im Rahmen einer Schularbeit, versuche ich unter anderem den Urknall chronologisch zu beschreiben. Aktuell stecke ich bei der Expansion des Universums fest. Nachdem Hubble ja die Rotverschiebung entdeckte, ist klar, dass sich alles von allem entfernt. Folglich sollte demnach auch alles mal beisammen gewesen sein. In einem anderen Blog hab ich erfahren, dass man die Entwicklung des Universums mit der Friedmann-Gleichung rückrechnen kann. Jetzt seh ich aber, dass Sie hier schreiben, dass das Universum keinen Rand besitzt oder besitzen müsse. wie kann man sich das vorstellen, wenn man von einer Ausdehnung von einem einzelnen Punkt ausgeht?
Wäre sehr dankbar für eine Antwort.
Mir scheint der Urknall verträgt sich nicht mit einem unendlich grossen Universum. Sogar die Erklärung in der Wikipedia lässt eigentlich kein unendlich grosses Universum zu. Dies zu obigem Textabschnitt:
Mit dem Big Bang verbinde ich intuitiv die Geburt des Universums aus einem Punkt. Wenn das Universum unendlich gross wäre, müsste es von Anfang an unendlich gross sein und der Big Bang könnte dann nur noch der Beginn der Expansion sein, nicht aber der Beginn des Universums.
Ich sehe schon, dass ich diesen Teil der Erklärung vorziehen sollte. In Kürze: Soweit ich sehen kann, redet Wikipedia zwar von einer Singularität, aber wohlweislich nicht von einem “Punkt”. Die Unterscheidung ist wichtig. Wenn man in einem der erwähnten Modelluniversum die Urknallsingularität betrachtet, dann ist sie unendlich groß. Das für uns beobachtbare Universum lässt sich allerdings auf einen Punkt in dieser unendlich großen Urknallsingularität zurückführen. Der Aussage “beim Urknall Skalenfaktor = 0” widerspricht das nicht; 0 mal unendlich oder 0 geteilt durch 0 sind nun einmal schon von der Mathematik her problematisch.
Aber das war wirklich nur die Kurzfassung; ich schaue mal, wie ich das am besten ausführlicher formuliere.
Nehmen die Abstände zwischen den Galaxien vielliecht nur deswegen zu, weil die Zeit vergeht und damit zwangsläufig a(t) zunimmt?
a(t) muss nicht zwangsläufig zunehmen – es gibt denkbare Fälle, in denen a(t) mit der Zeit kleiner wird.
Richtig ist aber, dass “a(t) nimmt mit der Zeit zu” in diesen Modellen untrennbar mit der Abstandsvergrößerung der Galaxien verknüpft ist. Warum a(t) zunimmt – also welche Kräfte und Einflüsse da am Werke sind – muss man dann im Laufe der weiteren Untersuchung klären.
Meine Frage zielt vielmehr noch darauf ab, ob es für uns (als Wesen, für die die Zeit linear verläuft und nur eine Richtung kennt) nicht zwangsläufig so aussehen muss, als ob sich das Universum ausdehnt. Die Beobachtung würde sich somit aus der Funktionsweise des Beobachters ergeben und entspricht in einem unendlichen Universum eventuell gar nicht der Realität?
Der Beobachter müßte aber gleich 2 Beobachtungen und eine 3. Frage erklären.
1. Die Galaxienhaufen entfernen sich voneinander, als ob dazwischen Raum entsteht.
2. Die Galaxien in den Haufen nehmen (noch) nicht an der Raumdehnung teil
3. Die Galaxien sind gravitativ gebunden, ist der Raum hier auch gebunden, oder bleiben die Galaxien an der “Stelle” und der “entstehende Raum darunter” dehnt sich auch weg?
OK, ich sammle mal Fragen für die nächsten Beiträge: Zum einen die Frage, ob “Raum entsteht” (das ist die Frage “Bewegung durch den Raum” vs. “Expansion des Raums”), zum anderen von Sphongle die (ja durchaus in der Literatur diskutierte) Frage, ob der kosmologische Zeitpfeil (in welche Zeitrichtung gibt es kosmische Expansion?) und der “normale” Zeitpfeil evt. zusammenhängen.
Was macht den Physiker eigentlich so sicher, dass der Kosmos expandiert und der Raum sich ausdehnt? Wäre es nicht genau so gut möglich, dass der Raum die einzige Konstante ist und alles in diesem Raum im gleichen Verhältnis zueinander schrumpft?
Intuitiv würde ich sagen, wenn alles schrumpfen würde, einschließlich der Elementarteilchen Planck-konstanten Lichtgeschwindigkeit etc. würde es zwar nicht auffallen, aber wir würden subjektiv immer noch eine Ausdehnung wahrnehmen.
Wenn eine der oben genannten Naturkonstanten gleich bliebe, hätten wir ein anderes Universum.
@Markus Pössel
Durch zeitabhängige Skalierung mit einer positiven, monoton wachsenden Funktion a(t) lässt sich gemäss
dist(t; x, y) := a(t) d(x,y)
praktisch jeder metrische Raum (M,d) scheinbar “expandieren”. Für M als Punktmenge hat diese Skalierung keine Konsequenzen, nur die Art und Weise der Abstandsmessung wird dadurch verändert. Und auch a(t) → 0 für fallendes t bedeutet kein Drama für M, einzig die Abstandsmessung entartet dabei.
Entsprechende Betrachtungen lassen sich auch für Raumzeiten verallgemeinern. Beispielsweise ist das Friedmann Universum mit Krümmungsindex k = 0 konform äquivalent zum Minkowski Raum, und wir haben
g = dt² − a²(t) (dx² + dy² + dz²) = a²(τ) η,
wobei τ die conformal time bezeichne. Die Bemerkung, »Das für uns beobachtbare Universum lässt sich allerdings auf einen Punkt in dieser unendlich großen Urknallsingularität zurückführen,« kann ich dabei, ehrlich gesagt, nicht recht einordnen.
Eine physikalische Rechtfertigung dafür, hier von Expansion zu sprechen, bedarf offenbar einer zusätzlichen Interpretation. Hingewiesen sei dazu insbesondere auf Walter Thirring, der in seinem Lehrbuch der Math. Physik, Bd. 2, die Friedmann Universen behandelt. Thirring spricht ausdrücklich nur von einer adiabatischen Expansion im Rahmen einer phänomenologischen Deutung als ein relativistisches Fluid, vgl. Bem. 4.4.11. (Seltsamerweise ging das bei englischen Übersetzung irgendwie verloren, der Verweis gilt explizit für das Original.)
Im übrigen hat Friedmann selbst in diesem Kontext nie von Expansion gesprochen. John Synge legt in seinem Gen. Rel. Buch dar, dass sich mit bezug auf Leuchtkraftabstand sinnvoll von Expansion reden lässt, er verweist dazu im weiteren auf Edmund Whittaker. Nach landläufiger Auffassung wird ja Lemaître als Entdecker der expandierenden Universums gehandelt, aber es ist jedenfalls mir nicht so klar, ob der da nicht etwas aus der Metrik herausgelesen hat, was die eigentlich gar nicht hergibt.
Chrys schrieb (4. März 2014 10:36):
> Durch zeitabhängige Skalierung mit einer positiven, monoton wachsenden Funktion a(t) lässt sich gemäss
> dist(t; x, y) := a(t) d(x,y)
> praktisch jeder metrische Raum (M,d) scheinbar “expandieren”.
Die Variablen “x” und “y” verstehen sich in diesem Zusammenhang übrigens als zwei unterscheidbare Elements der Menge “M“;
während sich “t” offenbar als Variable aus den Werten einer bestimmten geordneten Menge versteht (so dass “Monotonie” bzgl. der realen Zahlenwerte “a(t)” definiert wäre).
Was diese geordnete Menge (deren Elemente “t” genannt wurden), mit “Zeit” im Einsteinschen Sinne von Anzeigen jeweils eines bestimmten Beteiligten zu tun hätte, wäre allerdings noch zu verdeutlichen bzw. nachzuweisen.
> Für M als Punktmenge hat diese Skalierung keine Konsequenzen,
Für “M” als Menge sowieso nicht.
Und zwischen den verschiedenen durch “t“-Werte benannten (um nicht zu sagen: parametrisierten) metrischen Räume
“( M, dist_t )”
wären eben zueinander “skaliert isometrisch”;
mit allen dazugehörigen Konsequenzen, u.a.:
– je drei Elemente aus “M“, die bzgl. einer bestimmten dieser “Distanz”-Angaben zueinander gerade waren (abgesehen von “degenerierten a(t) == 0″), wären dann in allen mit verschiedenen “t“-Weisen benannten metrischen Räume ebenfalls zueinander gerade,
– je vier Elemente aus “M“, die bzgl. einer bestimmten dieser “Distanz”-Angaben zueinander eben waren (abgesehen von “degenerierten a(t) == 0″), wären dann in allen mit verschiedenen “t“-Weisen benannten metrischen Räume ebenfalls zueinander eben,
– je fünf Elemente aus “M“, die bzgl. einer bestimmten dieser “Distanz”-Angaben zueinander flach waren (abgesehen von “degenerierten a(t) == 0″), wären dann in allen mit verschiedenen “t“-Weisen benannten metrischen Räume ebenfalls zueinander flach.
> nur die Art und Weise der Abstandsmessung wird dadurch verändert.
Aber vielleicht hätte ja die CGPM eine Meinung dazu, ob es sich dabei auf alle Fälle auch um Messungen von “Länge” handelte, deren Messwerte als Vielfache von “Meter” ausgedrückt werden könnten; oder nur in manchen Fällen; oder gar nur in einem Falle; falls überhaupt.
p.s.
> John Synge legt in seinem Gen. Rel. Buch dar, dass […]
Dank Fernleihe werde ich in ein paar Tagen auch das in Synges Buch lesen können, was ich noch nicht schon auf einigen längst-vergilbten Kopieblättern (mit dem mir darin Allerwichtigsten) vorliegen habe.
@Frank Wappler
»Aber vielleicht hätte ja die CGPM eine Meinung dazu, ob es sich dabei auf alle Fälle auch um Messungen von “Länge” handelte, deren Messwerte als Vielfache von “Meter” ausgedrückt werden könnten; oder nur in manchen Fällen; oder gar nur in einem Falle; falls überhaupt.«
Die Kosmologen sind ausgesprochen grosszügig und einfallsreich, wenn es darum geht, was unter “Distanz” zu verstehen sein soll. Zur Übersicht ist diese Referenz vielleicht noch hilfreich; [Distance measures in cosmology].
Chrys schrieb (5. März 2014 12:13):
> Die Kosmologen sind ausgesprochen grosszügig und einfallsreich, wenn es darum geht, was unter “Distanz” zu verstehen sein soll.
Mögen sie ruhig.
Solche Großzügigkeit im Definieren verschiedener, keineswegs unbedingt kommensurabler “Distanz“-Messgrößen scheint aber mit erheblicher Knauserigkeit in der Darstellung entsprechender Mess- oder Erwartungswerte einherzugehen:
Diese Angaben erscheinen nämlich alle, so weit ich das erkennen kann, stets nur als reell-wertige
Vielfache von “(ein) Meter”;
ganz so als seien diese vielen verschiedenen, einfallsreich definierten, zugrundeliegenden
Messgrößen doch kommensurabel.
Ähnlich (aus Physikersicht laienhaft), wie die Leineweber früher sprichwörtlich ellen-lange Listen der verschiedensten menschlichen Auswüchse gleichermaßen “Elle” nannten …
p.s.
> Zur Übersicht ist diese Referenz vielleicht noch hilfreich; [Distance measures in cosmology].
Jedenfalls ist darin
(1) ausdrücklich von “Cosmography” die Rede; so dass also zumindest die begrifflichen Mittel zur unterscheidung von (vorrangiger) Geometrie/Kinematik und (nachgeordneter) Dynamik/Variationsrechnung anerkannt scheinen;
(2) auch eine gewisse reflektierte Selbsteinschätzung erkennbar; z.B. in
Ich fürchte allerdings, diese zugegebenermaßen für möglich gehaltene “ignorance” würde dabei wiederum derart kleinkariert aufgefasst, dass mit “h” von vornherein ein (positiver) reeller Zahlenwert verbunden würde; anstatt ein im Allgemeinen komplexer.
p.p.s.
HTML-Test:
“H<sub>0</sub> = 100 h km s<sup>>-1<>/sup> Mpc<sup>-1</sup>
=(is_rendered_as)=
H0 = 100 h km s-1 Mpc-1
@Frank Wappler
»… parameterizing our ignorance.«
Parametrisierte Ignoranz, das hatte ich noch gar nicht gesehen. Gefällt mir.
Chrys schrieb (7. März 2014 10:39):
> […] Gefällt mir.
Wie einfallsreich …
und sparsam.
p.s.
LaTeX(-MathJax)-Test:
“$latex \Deta_{\! H} \kern-1.15em _{^?} &s=3$”
=(is_rendered_as)=
$latex \Deta_{\! H} \kern-1.15em _{^?} &s=3$
Frank Wappler schrieb (7. März 2014 15:32):
> “$latex \Deta_{\! H} \kern-1.15em _{^?} &s=3$”
> =(is_rendered_as)=
> $latex \Deta_{\! H} \kern-1.15em _{^?} &s=3$
Was mangels SciLogs-Kommentarvorschau nur allzuleicht dafür gehalten werden könnte, dass
“$latex \Delta_{\! H} \kern-1.15em _{^?} &s=3$”
=(is_rendered_as)=
$latex \Delta_{\! H} \kern-1.15em _{^?} &s=3$
.
@Markus Pössel
Hallo.
Der Blogger Martin Bäker hat bei den ScienceBlogs einen Artikel darüber geschrieben, wie sich die Expansion auf Vorgänge in den Galaxien auswirkt.
Wenn der Raum sich ausdehnt
Mir kommt das falsch vor. Dort ist auch eine Kommentarschlacht entbrannt, über 70 Einträge in nur 5 Tagen.
Was sagst du dazu?
Wäre toll, wenn du die Zeit für eine Einschätzung finden würdest!