Vorweihnachtliches Statistikrätsel: Ein Trinkspiel
BLOG: Fischblog

Es ist zwar derzeit noch nicht besonders kalt, aber da wir die Feste feiern, wie sie fallen haben wir dieser Tage auf dem Altonaer Weihnachtsmarkt die Glühweinsaison eingeläutet. Bei solchen Gelegenheiten bleibt es normalerweise nicht beim Glühwein, und damit man sich beim zivilisierten unter-den-Tisch-Saufen nicht langweilt, dafür sorgen die verschiedenen mehr oder weniger anspruchsvollen Trinkspiele.
Als echte Nerds machen wir so etwas natürlich nicht, wir reden nur drüber. Zum Beispiel über die Gewinnchancen. Eigentlich kommt es darauf ja nicht an, und da man dabei unabhängig vom Ausgang diverse Drinks gereicht bekommt, ist sowie so jeder Teilnehmer ein Gewinner. Aber wir können besoffen ja bekanntlich über alles diskutieren, wenn auch etwas konfus.
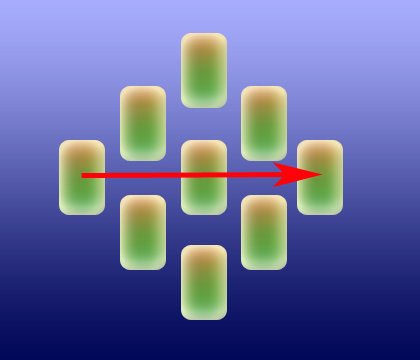
Das namenlose Spiel basiert auf einem gemischten Skatblatt mit 32 Karten, 16 rot, 16 schwarz. Es kommt nur auf die Farben an. Neun Karten des Blattes legt man rautenförmig und verdeckt aus, der Rest kommt auf einen ebenfalls verdeckten Stapel. Das Ziel ist es, durch Aufdecken der Karten von ganz links nach ganz rechts zu gelangen.
Bevor ein Spieler eine Karte aufdeckt muss er oder sie die Farbe dieser Karte raten. Wenn man richtig rät, darf man die Karte aufgedeckt lassen und mit einer Karte rechts daneben weitermachen. Wer fünf mal nacheinander richtig rät ist bei der ganz rechten Karte angelangt und hat gewonnen. Sobald man falsch rät, werden alle bisher aufgedeckten Karten weggelegt und aus dem Stapel wieder aufgefüllt, man fängt bei null wieder an – und man muss natürlich für jede Karte einen trinken. Wenn man nicht mehr auffüllen kann, weil der Stapel leer ist, hat man verloren (und deutlich über 20 Kurze intus).
Wie hoch ist die Chance zu gewinnen?
Näherungsweise ist die Wahrscheinlichkeit richtig zu raten bei jeder Karte 50:50. Soweit ich das sehe, ist damit jede aufgedeckte Karte zu dem Wurf einer fairen Münze äquivalent, und die Wahrscheinlichkeit, in einem Rutsch alle fünf Karten richtig zu raten ist für sich genommen (0,5)5 = 0,03125 oder etwa 3,1 Prozent. Aber man hat ja noch den Kartenstapel und damit mehrere Versuche.
Mit vier Karten, die bei einem erfolgreichen Durchlauf auf jeden Fall verdeckt bleiben, kann man im Verlauf des Spiels maximal 28 Karten aufdecken, bevor das Blatt aufgebraucht ist. Die Gewinnwahrscheinlichkeit entspricht also der Wahrscheinlichkeit, bei 28 Würfen mit einer fairen Münze eine Serie von fünf mal Kopf zu bekommen.
Ist das so? Spielt die Wahlmöglichkeit des Spielers wirklich keine Rolle?
Das ist aber noch nicht alles.
Bei den letzen fünf Karten im Spiel kann man nicht mehr auffüllen, wenn man falsch rät hat man sofort verloren. Dann allerdings hat man ja nicht mehr 28 Karten aufgedeckt, sondern z.B. nur noch 25. Ändert das etwas an der Gesamtwahrscheinlichkeit?
Außerdem kann man als Spieler ja mitzählen. Ist die erste Karte rot, sind im restlichen Blatt nur noch 15 rote und 16 schwarze Karten, die Wahrscheinlichkeit ist also etwas höher, bei der nächsten Karte schwarz zu erwischen. Und je weniger Karten im Spiel sind, desto größer wird der Effekt (wenn man fünf Karten hat und drei davon rot sind, ist die Wahrscheinlichkeit für rot 60 Prozent statt 50). Spielt das eine Rolle und wenn ja welche?
Ich bin gespannt auf eure Vorschläge.


Mehrere Faktoren
Prinzipiell würde ich sagen, dass dein Einwand so weit erstmal richtig ist: Wenn man mitzählt, dann kann man zumindest grob vorhersagen von welcher Farbe jetzt mehr Karten im Spiel sein sollten. Damit sollte es im Laufe des Spiels einfacher werden richtig zu raten, weil man besser abschätzen kann welche Farben noch im Spiel sind (allerdings wirkt der Alkohol-Pegel dem entgegen, wenn man schon 15+ Kurze intus hat).
Ohne jetzt genauer darüber nachgedacht zu haben gilt das glaube ich aber nur für die Positionen die bereits ersetzt wurden (das dürfte ganz ähnlich zum Ziegenproblem / Monty Hall sein, siehe: https://scilogs.spektrum.de/…-python-das-ziegenproblem ).
Die Karten die nie ersetzt wurden, weil man noch nie bis zu ihnen vorgedrungen ist, stammen noch aus der Wahrscheinlichkeitsverteilung ganz am Anfang als Rot und Schwarz relativ gleich verteilt waren (klar, auch hier wurde nicht zurückgelegt, aber es ist näher an einer Gleichverteilung dran, als die Karten die erst in der letzten Runde aus dem Stapel ins Spiel gekommen sind).
Man sollte seine Erwartungswerte also nur für die Karten anpassen die bereits ersetzt wurden. Bei einer Karte die erst letzte Runde ersetzt wurde sollte der Effekt dann auch größer sein als für eine Karte die bereits vor n Runden ersetzt wurde. Je länger es her ist, dass die Karte ins Spiel gekommen ist, desto näher sollte man wieder an 50:50 tippen, wenn ich nichts vergessen hab.
In dem Sinne: Prost
Stimmt…
man hat die Zusatzinformation nur bei den Karten, die schon ausgetauscht wurden.
odds?
das ist wie beim pokern (odds berechnung).
die kenntnis nutzt allerdings nur “longterm” niemal short term
ich hätte an urnenmodell ohne zuürcklegen gedacht beim nachziehen kombiniert mit baumdiagramm bei der raute
Stimmt
“man hat die Zusatzinformation nur bei den Karten, die schon ausgetauscht wurden.”
Stimmt, aber nur wenn man ziemlich besoffen ist.
Wenn bereits alle 16 roten Karten aufgedeckt wurden, gilt für die nicht ausgetauschten Karten immer noch 50 : 50?
Na dann mal Prost.
Das war ein Test, oder?
Joker hat natürlich recht (auch mit dem Pegel?) – wenn die Wahrscheinlichkeitsverteilung sich ändert, dann tut sie das für alle Karten, ob ausgelegt auf dem Tisch oder noch im Stapel (Bastian – die Wahrscheinlichkeiten beim Ziegenproblem ändern sich ja auch für die beiden übrig gebliebenen Türen, die nicht geöffnet wurden).
Die Wahrscheinlichkeit verändert sich beim Mitzählen allerdings nur marginal, solange man es nicht schafft, eine Farbe deutlich öfter als die andere aus dem Spiel zu ziehen.
Das Urnenmodell trifft zu (rote und schwarze Kugeln) Berücksichtigung der Reihenfolge, ohne Zurücklegen, Ziel: 5 richtige Tipps hintereinander, nach 32 Versuchen. Bei jedem Zug werden Wahrscheinlichkeiten für schwarz bzw. Rot neu vergeben (nach der Anzahl der verbliebenen Kugeln). Das muss für alle rot/schwarz-Zug-Kombinationen ermittelt werden. Dann hat man die Wahrscheinlichkeit, dass ein trinkfester Kopfrechenkünstler das Spiel gewinnt. Sitz grad nicht am Rechner, da ich dazu neige, solche Probleme per Algorithmus zu lösen (wahrscheinlich, weil ichs mathematisch nicht kann), sind mir gerade die Hände gebunden 🙂
Wahrscheinlicher als gedacht
Also, ich hab das ganze mal empirisch getestet (virtuell und ohne trinken). Das erstaunliche Ergebnis: Selbst uninformiert hat man eine 30%-Chance, das Spiel zu gewinnen. Das heißt, dass z.B. jemand, der stur immer nur “schwarz” tippt, in einem von drei Fällen gewinnt. Informiert steigt diese Wahrscheinlichkeit auf etwa 48%. Das heißt nun, dass der jemand z.B. immer nur “rot” tippt, wenn im Verlauf des Spiels mehr rote als schwarze Karten aufgedeckt wurde, ansonsten “schwarz”. Der Konsum von Kurzen ist allerdings in den meisten Fällen über den vom Gesundheitsminister empfohlenen Dosen anzusetzen.
Dem ganzen liegt das Urnenmodell zugrunde mit 16 roten und 16 schwarzen Kugeln. Die Urne kann bis auf die letzten 4 Kugeln (das sind die in jedem Fall auf dem Tisch verbleibenden Karten) leer gezogen werden. Diese 4 Karten sind übrigens der einzige Unterschied, der sich durch das Auslegen der Karten ergibt, ansonsten verhält sich alles so, als müsste man 5 Farben von einem Kartenstapel hintereinander richtig vorhersagen. Sie senken die Wahrscheinlichkeit, das Spiel zu gewinnen, übrigens um über 10% in der informierten Variante, ersparen einem aber dafür auch ein paar Kurze.
Bin gespannt, ob ich richtig liege (versucht mir mal das Gegenteil zu beweisen, @Fischblog und @Bastian ist das gestern nicht gelungen), schreibe vielleicht demnächst mal was drüber in meinem Blog (mit Häufigkeitsverteilung der getrunkenen Kurzen und Schrödingers Karte, Mathematische Formel wäre natürlich auch schön :).
Das ist deutlich mehr als ich erwartet hätte. Danke dafür.
Hast du auch Daten, wie viele Kurze man im Durchschnitt pro Durchgang trinken muss?
jo
Zunächst einmal: Zufall ist Unsicherheit. Und Sicherheit gewinnen wir durch das Aufdecken der Karten. Da ist es auch egal, ob die schon liegen oder ausgetauscht wurden. Daher ist es immer sinnvoll, die Farbe zu wählen, die bisher am seltensten aufgedeckt wurde.
Dann: Ich hab auch eine Simulation gemacht.
Strategie 1: immer schwarz. Gewinnchance: 30 %. Kurze pro Spiel (im Mittel): 22,5
Strategie 2: immer die bisher am wenigsten häufig aufgedeckte Farbe. Gewinnchance: 48 %. Kurze pro Spiel (im Mittel): 19
Korinthen
@DerMannMitHut
Da wir unabhängig voneinander simuliert haben, scheint die Gewinnchance ja zuzutreffen.
Allerdings habe ich nur 18 (informiert) bzw. 20 (uninformiert) durchschnittlich getrunkene Kurze als Ergebnis erhalten. Kann es sein, dass Du vernachlässigt hast, dass das Spiel schon dann verloren ist, wenn der Kartenstapel aufgebraucht ist und man die nächste falsche Vorhersage macht? Wenn man das (nach dann schon 24 getrunkenen Kurzen) realisiert, kann man einfach aufhören, weiter vorherzusagen und zu trinken. O.k., ist jetzt ein wenig spitzfindig. Aber korrekt. Vielleicht komm ich wirklich dazu, das Programm mal online zu stellen (Mein Paradethema: Veröffentlichung der Software erleichtert die Reproduktion von Ergebnissen). Ich teils mit.
noch kleinkarierter
@jhermes: Ja, das habe ich beachtet. Dann müssen wir tatsächlich mal die Software vergleichen.
Meine Sourcen:
1) Eine Zufalls-Simulation in node.js.
http://www.metstuebchen.de/…kspiel/trinkspiel.js
2) Eine vollständige Enumeration aller Rot-Schwarz-Kombinationen in C. Hier wird allerdings nur die Anzahl von vier “roten” Karten hintereinander gezählt.
http://www.metstuebchen.de/…nkspiel/trinkspiel.c
Grenzen der Kommunikation
@DenMannMitHut
Ja, den Trinkstopp hast Du definitiv beachtet (jedenfalls im Node.js-Programm, durch das C-Programm bin ich noch nicht ganz durchgestiegen). Bei Dir sind die Ergebnisse beider Programme aber gleich, ja? Mein java-Programm als Text hab ich mal hierhin gelegt –
http://jhermes.posterous.com/private/tnamilsnbE
Vielleicht findest Du den Fehler. Ergebnis bei mir ist 20.142737 Schnäpse (uninfomiert) und 18.054998 (mitzählend).
Und ja, ich weiss, Programmierstil und Veröffentlichungsmethode sind nicht gerade elegant. Machte so gerade die wenigsten Umstände.
Selbst gefunden
Hm, erst kommentiert, dann nachgedacht – mein Spieler weigert sich, überhaupt noch Schnäpse zu trinken, wenn er nicht mehr gewinnen kann. Das ist so natürlich nicht in Ordnung. Er muss ja zumindest die trinken, für die er schon Karten aufgedeckt hat. Hab den Fehler korrigiert und jetzt durchschnittlich 19,2 bzw. 21,7 Kurze raus. Jetzt bin ich aber auch still.
Neue Anregung
Betrachtet man den Fall, dass von beiden Farben gleich viele Karten vorhanden sind (z.B. beim Spielstart), könnte es dann nicht evtl. besser sein, wenn man die erste Karte richtig geraten hat, bei der Zweiten dieselbe Farbe zu nehmen? Man sehe:
P(4;5)=49,2%
p(4)=44,4% ’ 37,5%
p(5)=55,6% ’ 50%
P(3;6)=32,8%
p(3)=33,3% ’ 25%
p(4)=66,7% ’ 62,5%
P(2;7)=14,1%
p(2)=22,2% ’ 12,5%
p(7)=77,8% ’ 75%
P(1;8)=3,5%
p(1)=11,1% ’ 0%
p(8)=88,9% ’ 87,5%
P(0;9)=0,4%
p(0)=0% ’ 0%
p(9)=100% ’ 100%
daraus folgt:
p(schlechtes Ereignis)=36,3%
p(neutrales Ereignis)=27,4%
p(gutes Ereignis)=36,3%
E[p(schlechtes Ereignis)]=31,18%
E[p(gutes Ereignis)]=68,23%
IE[p(schlechtes Ereignis)]-50%I=18,72%
IE[p(gutes Ereignis)]-50%I=18,23%
Erklärung ’ = Wahrscheinlichkeit, danach dieselbe Farbe nochmal zu haben (unter denselben Bedingungen, Urnenmodell ohne Zurücklegen)
Man sieht, dass hierbei keine große Abweichung von 50% entsteht. Man erhält dadurch jedoch ein Ungleichgewicht zu Seiten der anderen Farbe, wodurch man diese beim nächsten Umdrehen mit mehr, statt bei dem verwendeten Ansatz, als 50% trifft. (Man hat auf die 5 Karten gerechnet eine 50-50-Entscheidung weniger.)
Diese höhere Chance sollte stärker ins Gewicht spielen als die niedrigere bei der zweiten Karte, welches die Gesamtchance erhöhen würde.
Kann einer der Statisten oder Spieltheoretiker das mal nachprüfen?
@ repli
Ich nehme die Rolle als Statist mal an.
Dein Gedanke erschien mir zuerst genial, dann einer Überprüfung wert, und nun zumindest nicht ganz falsch.
Wie mir jetzt erst klar wurde, kann man das Spiel auch so verstehen, dass man schon vor Beginn einer Runde sich auf alle Farben der 5 Karten festlegen muss. Zur zweiten Karte kommt man ja nur, wenn die Annahme für die erste Karte korrekt war, sonst muss man wieder von vorne anfangen. Also kann man sich auch schon vor dem ersten Umdrehen überlegen, was man für die zweite Karte wählen würde, wenn man mit der ersten Wahl recht hätte. Das gilt genauso für die 3., 4. und 5. Karte.
Es ist also nur eine Illusion, dass man im Verlauf einer Runde durch umdrehen von Karten einen relevanten Informationsgewinn bekäme. Die Information welche Karten bereits umgedreht wurden spielt nur vor der GESAMTEN Runde eine Rolle. Mit dieser Information kann man die wahrscheinlichste Häufigkeitsverteilung von rot und schwarz bei 5 Karten ermitteln. Zu Beginn ist dies 3:2 und man kann sich noch aussuchen welche Farbe die 3 sein soll, später könnte es 3:2 für eine bestimmte Farbe sein, oder dann sogar 4:1 oder 5:0.
Nachdem diese Verteilung ermittelt wurde, ist es egal in welcher Reihenfolge man die Farben während einer Runde tippt. Bei 4:1 für rot ist es also gleichwahrscheinlich zu gewinnen mit dem Tipp r,r,r,r,S oder S,r,r,r,r (oder eine der drei anderen Möglichkeiten).
Die von den anderen Kommentatoren beschriebenen Programme würden sich vermutlich zwischen r,r,r,r,S oder r,r,r,S,r entscheiden. Auch dies sind optimale Lösungen, aber eben nicht die einzigen.
Für den von dir beschriebenen Fall bedeutet dies, es ist kein Vorteil gleich am Anfang noch mal die selbe Farbe zu wählen, aber es ist auch kein Nachteil.
Ich kann leider nicht erkennen, wie man das von mir beschriebene Vorgehen dazu nutzen könnte, die Anzahl der zu trinkenden Schnäpse zu vermindern.
Jetzt trinke ich erst mal einen – einen Kaffee.
Hehe…
Damit kommen wir zu einer weiteren Frage: Gibt es Strategien, die über das einfache Auszählen der schon abgelegten Karten hinausgehen? (D.h. genau was Joker sagt: Kann man eine Fünfer-Serie als Ganzes angehen?)
Strategie ohne Zusatznutzen
Ich denke, dass Joker richtig liegt: Es gibt mehr ideale Lösungswege, als die stumpfen Mitzähler vom MannMitHut und mir beschreiten. Idealer werden sie aber dadurch nicht. Man kann so vorgehen, dass man sich am Beginn der Raute alle fünf Schritte hintereinander überlegt und seine rot/schwarz-Tipps danach verteilt. Sobald man falsch liegt, wird man ja wieder an den Anfang zurückgeworfen. Dann darf man allerdings nicht stur bei seinen Farb-Tipps bleiben, sondern muss sie wieder der dann bestehenden Wahrscheinlichkeitsverteilung anpassen.
Der Nutzen dieser Art zu spielen, wird mir allerdings nicht ganz klar – man muss sich dabei ja nicht nur die Anzahl der bereits aufgedeckten Farbkarten merken, sondern noch seine eigens ausgedachte Verteilung für bis zu fünf Karten im Voraus. Und nüchterner wird man bei dem Spiel ja nicht.
Die Aufdeckung einer Karte bleibt das Elementarereignis, welches das Verhältnis von Information und Unsicherheit bestimmt – Je ungleicher die Häufigkeit der Farben zwischen den aufgedeckten Karten, desto Information.
Diese kann durch das Aufdecken also auch abnehmen.
Bitte um Bedenkzeit
Und nach dem Kaffee kann ich mich auch schon selbst widerlegen.
Nehmen wir an es wären die letzten 9 Karten und nur noch eine schwarze dabei. Mit der von mir vorgeschlagenen Methode würde ich die 4:1 Verteilung als die wahrscheinlichere betrachten, und diese der 5:0 Verteilung vorziehen. Damit hätte ich zwar in 5 von 9 Fällen recht. Dann müsste ich aber noch die richtige Stelle treffen. Besser wäre es einfach zu hoffen, dass es sich beim aktuellen Spiel um eine aus den 4 von 9 Fällen handelt, in denen die schwarze Karte nicht unter den von mir gewählten ist. Das verbessert die Chance richtig zu liegen von 1:9 auf 4:9.
Die iterative Methode wäre hier eindeutig besser.
Ich glaub, ich leg mich wieder schlafen.
Ein Türchen öffnet sich
So, ausgeschlafen und Kaffee getrunken.
Bei einem Verhältnis von 3:2 gibt es 10 Möglichkeiten die Farben anzuordnen.
Bei einem Verhältnis von 4:1 gibt es 5
Bei einem Verhältnis von 5:0 gibt es 1
Mit den Wahrscheinlichkeiten richtig zu raten von 0,1; 0,2; bzw. 1,0
Erweitern wir mein letztes Beispiel (Noch 9 Karten) und schauen was ich machen müsste wenn 1, 2, 3 oder noch 4 schwarze Karten vorhanden sind. (Den Fall 0 rechne ich mal nach einigen Schnaps durch)
Für eine schwarze Karte hatte ich mir das ja schon überlegt:
Es gibt 9 Möglichkeiten, wie die Farbenverteilung ist (9 über 1).
a) 5 bei denen, 1 schwarze Karte unter den gewählten ist
b) 4 bei denen, 0 schwarze Karten unter den gewählten ist
Wenn ich Fall a) annehme, ergibt sich eine Gewinnwahrscheinlichkeit von
(5 / 9) * 0,2 = wenig
Für den Fall b)
(4 / 9) * 1,0 = besser
Deswegen hoffe ich auf Fall b) und rate 5 mal rot.
Bei zwei noch vorhanden Karten ändern sich die Verhältnisse:
Es gibt 36 Möglichkeiten (9 über 2)
a) 10 bei denen 2 schwarze Karten unter den gewählten ist (5 über 2)
b) 20 bei denen 1 schwarze Karte ist (5 über 1) mal (4 über 1)
c) 6 bei denen 0 (4 über 2)
a) (10 / 36) * 0,1
b) (20 / 36) * 0,2
c) ( 6 / 36) * 1
Ich nehme Fall c) und rate immer noch 5 mal rot
Bei noch 3 vorhandenen
Es gibt 84 Möglichkeiten (9 über 3)
a) 10 / 3 (5 über 3) mal (4 über 0)
b) 40 / 2 (5 über 2) mal (4 über 1)
c) 30 / 1 (5 über 1) mal (4 über 2)
d) 4 / 0 (5 über 0) mal (4 über 3)
a) 10 / 84 * 0,1
b) 40 / 84 * 0,1
c) 30 / 84 * 0,2
d) 4 / 84 * 1,0
Ich schätze, Fall c) ist jetzt der beste, und versuche deshalb zu erraten wo diese eine schwarze Karte steckt.
So, das Prinzip könnte eine Verbesserung versprechen. (Auch wenn ich den Fall mit 4 Karten nicht durchgerechnet habe) Was bleibt zu tun?
Man müsste mal ausrechen wie häufig am Anfang einer Runde jedes Verhältnis auftaucht. Wenn eine 3:2 Verteilung nicht mehr als doppelt so häufig ist, wie eine 4:1 Verteilung, sollte man auf eine solche Tippen. (Das könnte dann schon eine Verbesserung zur iterativen Strategie sein)
Dann müsste man ausrechnen, bei welchem Verhältnis im weiteren Spielverlauf sich die Strategie ändern sollte (und sich einen entsprechenden Spickzettel anfertigen).
Jetzt gehe ich noch einen Kaffee trinken, auf den Weihnachtsmarkt traue ich mich noch nicht.
@joker
Kannst Du nochmal ausführen, was genau durch die Strategie der 5-Karten-Vorhersage verbessert wird? Ich kann Deine Zahlenspiele zwar einigermaßen nachvollziehen, erblicke aber den Sinn des Ganzen nicht richtig. Spiele ich Deine Fälle mal mit meiner iterativen Maschine durch:
Eine schwarze Karte: Maschine tippt 5 * rot (wie bei Dir auch), Wahrscheinlichkeit ist auch die gleiche (wundersamerweise ergibt 8/9 * 7/8 * 6/7 * 5/6 * 4/5 auch 4/9)
Zwei schwarze Karten: Maschine tippt wieder 5 * rot (und liegt zu 6/36 richtig, wie bei Dir)
Drei schwarze Karten: Maschine tippt entweder rrrSr oder rrrrS (Je nach Implementation). Du hast mit Deinem Vorgehen noch die Möglichkeiten rrSrr rSrrr und Srrrr zur Verfügung. Das macht die Sache vielleicht abwechslungsreicher, erhöht aber weder die Wahrscheinlichkeit zu gewinnen, noch erspart es einem das Trinken von Schnäpsen, oder?
@ jhermes
Du hast vollkommen recht, bisher ist noch gar nichts gezeigt. An den 9 Karten zu Schluss habe ich nur das Prinzip entwickelt. Es könnte eine Verbesserung sein, muss es aber nicht. Man muss es erst einmal für den Anfang des Kartenstapels durchrechnen und schauen ob sich ein Unterschied zur anderen Strategie ergibt.
@ jhermes
In der ersten Runde scheint die 5-er Strategie keinen Unterschied zu machen. Und es kann natürlich für weitere Runden genau das eintreten, was du schon zum Ende des Spiels gezeigt hast, dass beide Strategien auf das gleiche herauslaufen. Wenn der Unterschied so groß wird, dass die 5-er Strategie ein 4:1 Verhältnis wählt, dass dann auch die iterative Strategie 4:1 raten würde.
Am Ende des Spiels könnte es doch einen Unterschied geben, wenn schon nicht bei der Gewinnerwartung, dann doch bei den getrunkenen Schnäpsen. Wenn ich mich nicht verrechnet habe, so auf die schnelle, ist der Erwartungswert an Alkoholkonsum etwas geringer, wenn man die eine schwarze Karte am Anfang vermutet.
Ob das allerdings auch ein Vorteil sein kann (wenn man weniger Schnaps überhaupt als Vorteil ansieht), solange noch Karten, und damit potentielle Schnäpse, wieder aufgefüllt werden, glaube ich eher nicht.
@ Lars
Gibt es noch einen kleinen Hinweis? Die Weihnachtsmarktsaison ist kurz und die Polizeikontrollen sind streng.
@joker
ich muss da leider passen, hab auch nicht mehr Infos als ihr. Intuitiv halte ich es zumindest für möglich, dass bestimmte Fünferkombinationen über alle möglichen Spielverläufe möglicherweise wahrscheinlicher sind und deswegen erfolgversprechendere Hypothesen darstellen könnten.
@ all
Verbesserungsmöglichkeiten sehe ich noch durch die Wegewahl gegeben.
In der zweiten (und vierten) Reihe liegen zwei Karten, die entweder rr, rS, Sr oder SS sind. Wenn ich eine davon umdrehe, und die Farbe ist rot, müsste für die andere Karte eine Wahrscheinlichkeit von 2:1 für schwarz als Farbe gelten.
In der dritten Reihe komme ich nach ähnlichen Überlegungen dazu, bei der zweiten Wahl zunächst schwarz zu wählen (9:5), falls die ersten Karte rot war, aber wenn beide doch rot sind, bei der dritten sogar mit 3:1 sicher zu sein, dass es sich um schwarz handelt.
Wende ich das Prinzip hier korrekt an?
Wenn ja, gilt das auch wieder nachdem Karten aus den Reihen ersetzt wurden?
Hier wird aber auch keine Ruhe gegeben..
@Fischblog Meine Intuition, die ich hier von Anfang an versuche zu verteidigen, ist die, dass die Lage der Karten auf dem Tisch völlig irrelevant ist und dass es keinen besseren (d.h. häufiger gewinnenden und weniger Schnaps trinkenden) Spieler gibt als die Zählautomaten vom MannMitHut und mir. Das liegt am unverrückbaren Elementarereignis (s.o.). Beim Beweis des Gegenteils bräche mein intuitiv-wahrscheinlichkeitstheoretisches Weltbild zusammen. Und kommt mir nicht mit dem Ziegenproblem – der gewichtigste Unterschied ist hier, dass es keinen informierten und handelnden Moderator gibt.
@Joker Nein, Du wendest das meiner Meinung nach nicht richtig an. Ich bin auch nur Freizeit-Stochastiker, mir aber ziemlich sicher, dass Du die Positionen der Karten beachten musst. Das heißt, Du liegst richtig, dass zwei nebeneinander liegende Karten entweder rr, rS, Sr oder SS (schlimmes Kürzel) sind. Wenn Du jetzt aber sagen wir die linke Karte aufdeckst und diese rot ist, so bleiben nur die ersten beiden Möglichkeiten, also rr und rS übrig (ansonsten würde ein erster Würfelwurf auch immer einen zweiten beeinflussen). Die rechte Karte ist also zu jeweils 50% rot oder schwarz. Damit ist auch die Dreierreihentheorie hinfällig. Einverstanden? Ich hab übrigens ne Menge Spass an der Sache (natürlich nur solange ich recht behalte).
Ok, Ok
Ich bin wieder nüchtern.
War wirklich keine gute Idee.
Nüchtern sein?
Stimmt, das lohnt sich nicht wirklich… :-p
Ich fürchte jhermes hat tatsächlich in den wesentlichen Punkten Recht…
Nachgerechnet
Also, ich hab mal ein bisschen nachgedacht und gerechnet. Das alles ohne zu formal zu werden.
1. Wir wissen, dass man seine Taktik für den Fünfer am Anfang festlegen kann (da man innerhalb eines Fünfers kein Wissen gewinnen kann, es sei denn, man verliert).
2. Es reicht, die Taktik von der Anzahl der restlichen roten und schwarzen Karten abhängig zu machen (da die Position der Karten auf dem Tisch irrelevant ist).
3. Für eine Taktik ist die Reihenfolge von rot und schwarz innerhalb eines Fünfers irrelevant (da es sich um Urnenspiel mit Ziehen ohne Zurücklegen handelt).
Damit kann man die Taktik als Anzahl der zu tippenden roten Karten definieren. (Beispiel: “Taktik 3” bedeutet: “Zweimal schwarz und dreimal rot wählen”, konkret könnte das rrSrS, SSrrr usw. sein).
Sei jetzt S die restliche Anzahl der schwarzen Karten und R die restliche Anzahl der roten. Wenn man nun für jede mögliche Kombination von Restkarten (also für S=0..16, R=0..16, S+R>=9) ausrechnet, welche der 5 Taktiken welche Gewinnwahrscheinlichkeit hat, so kann man die Taktiken mit der maximalen Gewinnwahrscheinlichkeit heraussuchen. Das Maximum ist dabei nicht immer eindeutig. Eine mögliche Strategie lautet:
S-R >= 5: Taktik 0
S-R = 4: Taktik 1
S-R = 3: Taktik 1
S-R = 2: Taktik 2
S-R = 1: Taktik 2
S-R = 0: Taktik 3
S-R = -1: Taktik 3
S-R = -2: Taktik 4
S-R = -3: Taktik 4
S-R
Abgeschnitten
(… und hier der Rest meines Postings:)
S-R >= 5: Taktik 0
S-R = 4: Taktik 1
S-R = 3: Taktik 1
S-R = 2: Taktik 2
S-R = 1: Taktik 2
S-R = 0: Taktik 3
S-R = -1: Taktik 3
S-R = -2: Taktik 4
S-R = -3: Taktik 4
S-R
(args, HTML Gedöns, nochmal!)
S-R kleiner gleich -4: Taktik 5
Das entspricht aber genau der einfachen Strategie, jeden einzelnen mitzuzählen und bei Gleichstand “rot” zu wählen.
Das bedeutet für mich:
a) Wenn die Annahmen 1) bis 3) richtig sind, handelt es sich um eine optimale Strategie.
b) Die Strategie entspricht dem intuitiven “Mitzählen und häufigere Farbe wählen”.
c) Es gibt mehrere optimale Strategien; sie unterscheiden sich in der Wahl bei Gleichstand der Kartenanzahl
@DerMannMitHut und andere 5-Karter
Hast Du Deine Strategie mal selbst simuliert? Ich bekomm für 1 Mio Trinkspieler nämlich folgendes Ergebnis:
Naive Strategie (immer irgendwas tippen, z.B. immer rot):
Gewinnchance: 0.30
Schnäpse: 21.20
Meine Strategie (Farben zählen, vor jeder Karte entscheiden):
Gewinnchance: 0.48
Schnäpse: 18.92
Deine Strategie (laut Post, 5 Karten im Voraus):
Gewinnchance: 0.44
Schnäpse: 19.29
Der Unterschied ist nicht besonders groß, ich habe aber offenbar bessere Chancen, zu gewinnen (na gut, während Du bessere Chancen auf mehr Schnäpse hast). Code ist noch nicht kommentiert, kann ich aber bei Interesse online stellen (wieder Java, diesmal aber objektorientiert).
Schönes Wochenende (am Punschstand?)
Pingback:Russisch Roulette – Highlander Edition | TEXperimenTales
Pingback:Russisch Roulette – Highlander Edition | TEXperimenTales