Auf Tuchfühlung mit ALMA, 3. Teil: Das Weltall im Submillimeterteleskop
BLOG: Himmelslichter

Mit seiner Long-Baseline-Konfiguration erreicht ALMA ein Winkelauflösungsvermögen, dass es mit den weltbesten Teleskopen aufnehmen kann. In der im Herbst 2014 getesteten Variante lag das Auflösungsvermögen bei etwa 35 Millibogensekunden. Zum Vergleich: ein 8,2m-VLT-Teleskop erreicht (ohne Interferometrie aber mit adaptiver Optik) etwa 50, das Hubbleteleskop (mit kleinem Spiegel und ohne adaptive Optik, aber eben auch ohne störende Erdatmosphäre) 40 Millibogensekunden. Was das konkret bedeutet, darum soll es in diesem dritten und letzten Teil der ALMA-Blogserie gehen. (Hier geht es zurück zu Teil 1 und Teil 2.)
Bevor es dafür an ein paar beeindruckende Beispiele geht, zuerst etwas Physik (das ist schließlich keine Spaßveranstaltung hier). Man kann sich auf einem Blatt Papier schnell klar machen, dass die wahre Größe g eine Objekts, dass unter einem Sehwinkel α erscheint, umso größer ist, je weiter das Objekt vom Betrachter entfernt ist. Man kann auch die Wikipedia fragen:
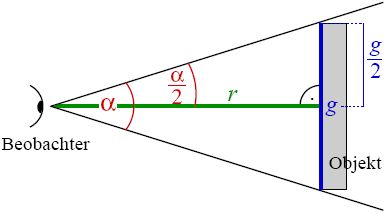
Das gilt genauso für unser Auflösungsvermögen, dass ja definiert ist als der Sehwinkel, unter dem zwei nahe beieinander liegende Objekte gerade noch getrennt dargestellt werden.
Was ein (als Winkel angegebenes) Auflösungsvermögen konkret (also etwa als Längenangabe in Kilometer) bedeutet, hängt also davon ab, wie weit das beobachtete Objekt entfernt ist.
Und damit zu den Beispielen.
Der Asteroid Juno war am 19. Oktober 2014 rund 295 Millionen Kilometer von der Erde entfernt, als ALMA den rund 300 Kilometer großen Felsbrocken vier Stunden lang ablichtete. Die Antennen standen dabei maximal 13 Kilometer voneinander entfernt, das ergab ein Winkelauflösungsvermögen von 42 Millibogensekunden. Um aus diesen Angaben das Auflösungsvermögen in Kilometern auszurechnen, braucht man nur etwas Trigonometrie. Ich spare mir das hier, im Wikipediaartikel steht genug dazu. In diesem Fall ergibt sich ein “reales” Auflösungsvermögen von 60 Kilometern – das reicht aus, um die Form des Asteroiden während seiner siebenstündigen Rotation abzubilden.
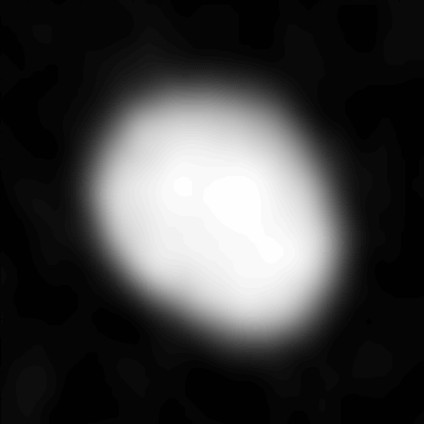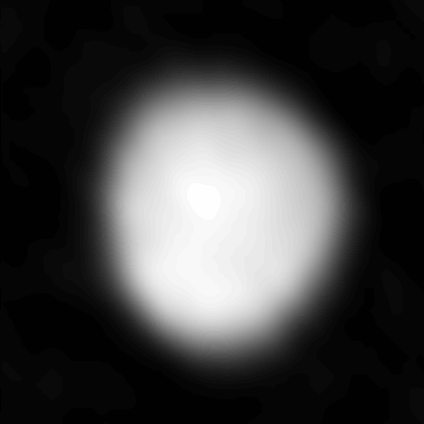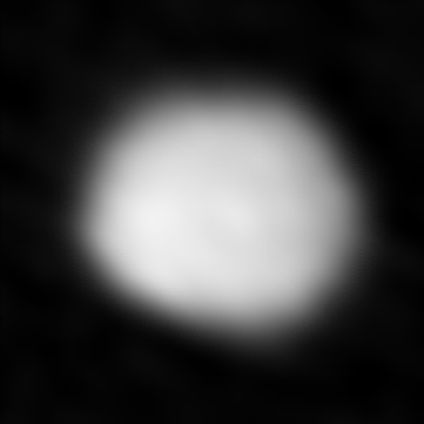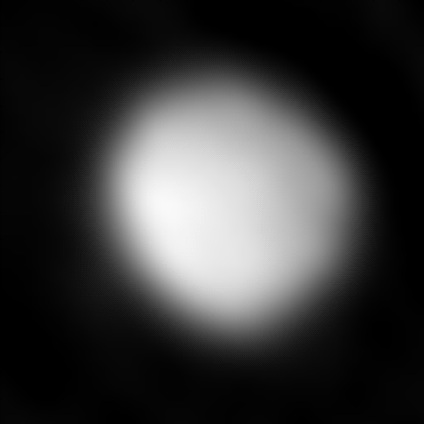
Das wirft Sie jetzt noch nicht um? Ok – unscharfe Bilder von Juno gibt es schon länger, aber eben in anderen Wellenlängen. Optische Bilder zeigen das von der Asteroidenoberfläche zurückgeworfene Sonnenlicht – ALMA dagegen die Wärmestrahlung die von dem Asteroiden ausgehende Wärmestrahlung. Damit können die Astronomen neues über die Eigenschaften und Zusammensetzungen von Asteroidenoberflächen lernen. Wer sich für das wissenschaftliche Paper interessiert, findet es hier.
Kommen wir dann zu meinem persönlichen Favoriten, der die Leistungsfähigkeit ALMAs besser deutlich macht als jedes andere Beispiel bisher.
Sehr viel weiter von der Erde entfernt, nämlich rund 450 Lichtjahre, ist der Stern HL Tauri. HL Tauri ist ein sehr junger Stern – sein Planetensystem ist noch in der Entstehung begriffen. Umgeben ist er von einer sogenannten protoplanetaren Scheibe, in der vermutlich Planeten entstehen. Und wenn man sich das ALMA-Bild anschaut, kann man sich das ziemlich gut vorstellen:

Das Hintergrundbild ist eine Aufnahme des Hubbleteleskops, die ALMA-Aufnahme ist das Inset rechts oben. Für diese Beobachtungen standen die Antennen bis zu 15,24 Kilometer auseinander, das Winkelauflösungsvermögen erreichte 35 Millibogensekunden. Damit übertraf ALMA erstmals Hubble, ein Grund mehr, beide Bilder nebeneinander zu zeigen.
In 450 Lichtjahren Entfernung entspricht das Auflösungsvermögen von 35 Millibogensekunden rund fünf astronomischen Einheiten, also dem fünffachen der Entfernung Erde-Sonne oder 750 Millionen Kilometer. Deutlich sieht man dunkle Lücken in der protoplanetaren Scheibe aus Gas und Staub – genau hier entstehen die Planeten. Kein anderes ALMA-Bild begesitert mich mehr als dieses: Wir können einem Sonnensystem bei der Entstehung zugucken! (Hier gehts wieder zur Originalveröffentlichung)
Das folgende Bild zeigt den Vergleich des HL-Tauri-Protosystems mit unserem eigenen Sonnensystem. Die äußere der eingezeichneten Planetenbahnen im rechten Bild ist die von Neptun, die Scheibe um HL Tauri erstreckt sich fast dreimal so weit ins All:

Schaut man mit der gleichen Antennenkonfiguration noch viel weiter ins All, bleibt das Winkelauflösungsvermögen gleich, das “reale”, in Kilometern gemessene, natürlich nicht. Es wird größer, so groß, dass man es besser nicht in Kilometern, sondern Lichtjahren angibt. Als Beispiel dient die Galaxie SDP.81: sie ist rund 12 Milliarden Lichtjahre entfernt. Auch sie hat ALMA angepeilt und das hier gesehen:

Was man sieht, ist das leuchtende Gas der Galaxie – ALMA macht ja bekanntlich keine Aufnahmen im optischen Licht, in dem die Sterne leuchten. Statt dessen sieht man die kühlen Gasmassen zwischen den Sternen. ALMAs Antennen waren ebenfalls rund 15 Kilometer von einander entfernt, die Auflösung erreichte sogar 23 Millibogensekunden: Rekord! (Es ist etwas kleiner noch als bei HL Tauri, aber das liegt an der unterschiedlichen Wellenlänge der verwendeten Strahlung. ALMA kann nicht nur in einer, sondern in mehreren Frequenzbändern beobachten.)
Auf 12 Milliarden Lichtjahre entspricht 23 Millibogensekunden rund 590 Lichtjahre. Klingt nach viel – aber wir reden hier ja auch von einer Entfernung von zwölf Milliarden Lichtjahren… (Originalveröffentlichung)
Fehlt noch was? Achja, SDP.81 wird von einer viel näheren Galaxie zu einem lehrbuchhaften Einsteinring gelinst, aber das haben Sie ja wahrscheinlich schon gemerkt.
Je größer die Basislinie, also die Entfernung zwischen den Antennen, desto besser das Auflösungsvermögen, desto kleiner die Strukturen, die ALMA noch darstellen kann. Da wird die Frage erlaubt sein, warum die Antennen dann noch verschiebbar sind – weshalb montiert man sie nicht fest, und zwar so, dass sie stets die größte Entfernung zueinander haben? Kleinere Basislängen machen das Teleskop doch leistungsschwächer, oder?
Jein. Größere Basislängen verbessern zwar das Auflösungsvermögen, verschlechtern aber einen anderen Parameter, der ebenfalls wichtig ist: die so genannte Maximum Recoverable Scale (MRS), also frei übersetzt die “maximale beobachtbare Skala”. Was es damit auf sich hat, sieht man am besten an einem anderen ALMA-Bild der Long Baseline Campaign, das etwas anders ist als die drei gezeigten.
Knapp 400 Lichtjahre entfernt von der Erde, in Richtung des Sternbilds Walfisch, befindet sich der außergewöhnliche Riesenstern Mira (Omikron Ceti), der eigentlich ein Doppelsternsystem ist. So sieht ihn ALMA:

Wenn Sie auf diesem Bild verzweifelt nach dem Stern Mira suchen, haben Sie vorhin nicht aufgepasst: ALMA sieht keine Sterne, sondern die kühlen Staubwolken dazwischen. Die bizarre Nebelstruktur im Bild entsteht durch das komplexe Zusammenspiel der Sternwinde von Mira A (einem roten Riesenstern) und Mira B (einem weißen Zwerg). Mira A ist ein alter Stern, der seine äußeren Gashüllen eher gemächlich in das umgebende Weltall bläst. Mira B dagegen, der Mira A in etwa doppeltem Abstand Sonne-Neptun umkreist, verhält sich völlig anders: Er ist heiß und sehr dicht, sein Sternwind weht energiereich und stürmisch.
Au dem ALMA-Bild erkennt man die von Mira A abgestoßenen Gaswolken und darin eine vom stürmischen Mira-B-Wind gerissene, herzförmige “Blase”. Diese Blase soll in den letzten 400 Jahren entstanden sein – in astronomisch extrem kurzer Zeit. (Hier gehts wieder zur Orignalveröffentlichung.)
Alles schön und gut, aber was heißt das nun für die “Maximal Recoverable Scale”? Ganz einfach: Hätte ALMA dieses Objekt in der gleichen Konfiguration wie Juno, HL Tauri oder SDP.81 aufgenommen, hätte es zwar ein Auflösungsvermögen von vielleicht nur fünf astronomischen Einheiten erreicht (ähnlich wie bei HL Tau), aber nur für einen kleinen Ausschnitt des Bildes. Die gesamte Gaswolke ist nämlich über etliche Bogensekunden am Himmel verteilt. (Es ist schade, dass zum Bild keine Skala mitgeliefert wurde, der Maßstab dürfte zwischen dem oben gezeigten Hubblebild und dem ALMA-Bild von HL Tauri liegen.)
Heißt: Das Objekt ist zu ausgedehnt, um mit maximaler Auflösung vollständig in einer einzelnen Beobachtung “gesampled” zu werden. Je größer die Basislänge eines Interferometers, desto größer ist zwar sein Auflösungsvermögen, desto kleiner aber sind im Gegenzug die größten Strukturen, die das Interferometer noch abtasten kann – eben die MRS. Bei gewissen Objekten wie bei Mira (oder wissenschaftlichen Fragestellen) kommt es nicht so sehr auf das Auflösungsvermögen an, sondern auf die MRS – die Objekte sind sonst nicht beobachtbar.
Das ist in gewisser Weise vergleichbar dem Wechselspiel aus Vergrößerung und Gesichtsfeld, das Amateurastronomen gut kennen: Eine schwache Vergrößerung zeigt weniger Detail, erlaubt aber die Beobachtung ausgedehnterer Objekte.
ALMA kann dank seiner versetzbarer Antennen beides: hohe Auflösung und großes MRS – nur nicht beides zur gleichen Zeit. Damit man nicht ständig Antennen vesetzen muss (ein Knochenjob, irgendjemand muss Otto und Lore ja auf 5000 Metern bedienen) werden die eingehenden Beobachtungsanträge entsprechend sortiert. Für Beobachtungen, bei denen es praktisch nur aufs MRS und nicht so sehr auf die Auflösung ankommt, kann man nur die 16 Antennen des Atacama Compact Array (ACA) nutzen: die stehen dicht beieinander und lassen sich separat vom restlichen Netzwerk speziell für ausgedehnte Objekte nutzen, etwa Gaswolken wie bei Mira oder nahe Galaxien. Zum ACA gehören die zwölf Sieben-Meter-Antennen sowie vier der 12-Meter-Antennen.
Für das Mira-Bild wurden Basislinien bis zu 450 Meter genutzt, weit weniger als bei den anderen Bildern. Auch das ACA wurde eingesetzt, hier lag die maximale Basislänge sogar nur bei 45 Metern. Das entsprach einer MRS von sechs bzw. neun Bogensekunden. Die Beobachtungen fanden teilweise bereits im Februar bis Mai 2014, die mit dem ACA sogar schon im Oktober 2013 statt, als noch gar nicht alle Antennen vor Ort waren. Astronomen sind ungeduldig.
Die Sache mit dem Auflösungsvermögen und dem MRS ist in diesem Video (englisch) noch mal schön erklärt. Das Video richtet sich zwar an Astronomen, die ihre Beobachtungsanträge an das ALMA-Team richten wollen, aber Sie sind jetzt gut gerüstet, es zu verstehen.
Damit endet dieser dreiteilige Blogbericht. Falls er unterhaltsam war und dennoch etwas Hintergrundwissen zu diesem einzigartigen Projekt geliefert hat, hat er seinen Zweck erfüllt. Zum Abschluss, und weil meine Festplatte überquillt, noch ein paar Bilder unseres Besuchs.






Danksagung und Offenlegung: Der Besuch bei ALMA war Teil eines viertägigen Pressebesuchs aus Anlass des E-ELT-Blasts im Juni 2014. Mein Dank gilt der ESO, die diesen Besuch möglich gemacht hat, allen daran Beteiligten und insbesondere Laura Ventura vom ESO-Team für ihre hochkompetente, stehts hilfreiche und freundliche Betreuung. Die Kosten der Reise innerhalb Chile hat die ESO übernommen.


Das mächtigste und flexibelste Array von Radioteleskopen ist also rekonfigurierbar und besteht aus mobilen Teleskopen. Mit jeder Rekonfiguration kann ein solches Array von Radioteleskopen optimal auf das abzubildende Objekt aubgestimmt werden.
Am einfachsten wäre eine Rekonfiguration, also eine andere geometrische Anordnung von Teleskopen im Weltraum zu erreichen. Heute gibt es allerdings noch kaum grössere Radioteleskope im Weltraum, was daran liegt, dass ein Radioteleskop deutlich grösser sein muss als ein in den Leistungen vergleichbares optisches Teleskop. Ein grösseres Teleskop im Weltraum bedeutet heute aber auch die Notwendigkeit mehr Material in den Weltraum zu transportieren, womit solche Teleskope durch die Transportkapazität heutiger Raketen beschränkt werden. Es ist absehbar, dass diese Grenze in Zukunft überwunden werden kann indem die eigentliche Radioschüssel erst im Weltraum zusammengesetzt wird – und zwar aus MIkrofilamenten, die praktisch nichts wiegen. Dazu bräuchte es eine Art 3D-Drucker oder mindestens einen Montageautomaten.
Pingback:Auf Tuchfühlung mit ALMA, 2. Teil: 66 Augen sehen mehr als zwei › Himmelslichter › SciLogs - Wissenschaftsblogs
Punktaufllösungsvermögen von ALMA bei Junobeobachtung berechnen ohne Pythagoras oder Trigonometrie
Jeder Grundschüler, der weiss, was ein Winkel und ein Kreisbogensegment ist, kann den in diesem Blogbeitrag durchgerechneten kleinsten Punktabstand berechnen, den ALMA auf Juno auflösen kann, ohne dass er dazu Wikipedia oder irgend eine Formel konsultieren muss. Hier nun, wie er dazu kommt:
Wir betrachten die Länge des Kreisbogensegments, das einem sehr kleinen Winkel im Abstand 1 Meter gegenübersteht. Vergrössern wir den Abstand von 1 m auf 2 Metern, dann verdoppelt sich die Länge dieses Bogensegments, denn alle Strecken eines Objekts verdoppeln sich, wenn man das Objekt auf das doppelte streckt. Vergrössern wir den Abstand gar auf den Abstand Erde/Juno, dann verlängert sich das Bogensegment um den Faktor 295 Milliarden, denn Juno ist so viele Meter von der Erde entfernt. Dieses Bogensegment, das sich nun bei Juno befindet, können wir auch als gerade Strecke betrachten, denn bei einem sehr kleinen Winkel ist ein Kreisbogensegment nicht von einem Geradenstück zu unterscheiden. Nun müssen wir nur noch die Länge des Kreisbogenstücks in einem Meter Abstand vom Zentrum des sich öffnenden kleinsten Winkels kennen, den ALMA auflösen kann. Nach den Angaben im Blog beträgt dieser Winkel 42 Millibogensekunden. Diesen Winkel müssen wir nun umrechnen in die Länge des Kreisbogens in einem Meter Abstand vom Punkt wo die beiden Strahlen des Winkels entspringen. Dazu benützen wird die Konversion (Umwandlung) Millibogensekunden zu Bogenmass, was auf Englisch Convert milliarcsecond to radian heisst. Resultat: 42 Millibogensekunden ergeben 0.0000002036217461 Bogenmass. In 1 Meter Abstand vom Winkelursprung ist die Bogenlänge, die zum Winkel gehört also 0.0000002036217461 Meter lang
Um die Länge des entsprechenden Bogens (der entsprechenden Seitenlänge) in der Entferung von Juno zu berechnen, müssen wir nun diese Länge mit dem Abstand zu Juno multiplizieren, was wir mit folgender Rechnung tun: Länge des Bogens bei Juno = 0.0000002036217461 Meter * (Abstand zum Juno in Metern)
was konkret auf folgende Muliplikation hinausläuft: 0.0000002036217461 * 295000000000 .
Resultat ist: 0.0000002036217461 * 295’000’000’000 = 60068.4150995
Wir können also mit ALMA zwei Punkte auf Juno unterscheiden, die 60068 Meter voneinander entfernt sind. Das sind 60 Kilometer.
Zusammengefasst: Die Winkelauflösung in Bogenmass multipliziert mit dem Abstand des Zielobjekts ergibt den minimalen Abstand zwischen zwei Punkten auf dem Zielobjekt, den wir auflösen können.
Danke fürs Nachrechnen! Dann stimmt also, was in der Pressemitteilung steht (sollte man immer überprüfen, ich war nur ein bisschen faul 😉