Die rauhen Welten des Martin Hairer – Teil 1
BLOG: Heidelberg Laureate Forum


Martin Hairers Vortrag an Dienstag, “Taming infinities” – Unendlichkeiten zähmen – bot einen faszinierenden Überblick über einiges an dem, was der Mathematiker erforscht – und wofür er 2014 auch die Fields-Medaille bekommen hat.
Hairers Arbeit verbindet Zufallsprozesse und das wichtigste Instrument der Mathematiker zum Beschreiben von Änderungen – Differentialgleichungen – andererseits. Für mich war das ein völlig neues Themengebiet, das ich in den letzten Tage versucht habe, zum einen in groben Zügen zu verstehen, zum anderen verständlich zu beschreiben. Ganz ohne Differential- und Integralrechnung wird es dabei allerdings nicht gehen.
Warnhinweis: Ich schreibe üblicherweise über Themen, die ich deutlich besser verstehe als dieses hier. Wo meine Vereinfachungen (oder Aussagen) in die falsche Richtung gehen, bitte ich um Korrekturhinweise bzw. Ergänzungen fachlich vorbelasteter Leser in den Kommentaren!
Damit aber jetzt bis zur Unendlichkeit, und noch viel weiter.
Glatte Physik
In der klassischen Physik wird die Art und Weise, wie sich die Welt ändert, durch sogenannte Differentialgleichungen, die typischerweise Beschleunigungen und Geschwindigkeiten (mathematisch also: zweite bzw. erste Ableitungen) von Teilchen mit der Wirkung von äußeren Einflüssen verbinden.
Für die Funktionen, die dabei z.B. den Ort eines Teilchens in Abhängigkeit von der Zeit beschreiben, wird üblicherweise vorausgesetzt, dass sie keine plötzlichen Sprünge machen, mathematisch gesagt: dass sie stetig sind. Dieselbe Annahme wird für die Änderungsrate der Funktionen gemacht (Differenzierbarkeit) und für deren Änderungsrate, und oft ganz einfach für alle Änderungsraten höherer Ordnung (Änderung der Änderung der Änderung der…). Solche Funktionen heißen unendlich oft differenzierbar oder glatt.
Mathematiker sind bemüht, ihre Theoreme mit so wenig und so schwachen Annahmen wie möglich zu beweisen. Physiker sind da verschwenderischer, und arbeiten oft mit glatten Funktionen, weil es bequem und einfach ist. Für die Physik macht die Glattheits-Annahme in der Regel keinen Unterschied – also warum es komplizierter machen als nötig?
Was bewirkt die Brown’sche Bewegung?
Meist kommen die Physiker damit sogar durch, aber in einigen Fällen nicht. Das berühmteste Beispiel für einen Fall, in dem es gar nicht klappt, dürfte die Brown’sche Bewegung sein. Sie wurde erstmals in der ersten Hälfte des 19. Jahrhunderts von dem Botaniker Robert Brown beobachtet: Brown betrachtete durch sein Mikroskop im Wasser schwimmende Pollenkörner, und ihm fiel auf, dass diese sich ohne direkt ersichtlichen Grund unruhig bewegten, jedes Teilchen auf einer ziellosen Wanderung mit vielen Richtungsänderungen.
Der erste, der quantitativ zeigte, wie diese Bewegung zustande kommt, war Albert Einstein – in einer der Öffentlichkeit weniger bekannten Veröffentlichung aus seinem “Annus mirabilis” 1905: Die Bewegung ergibt sich, weil die Pollenkörner immer und immer wieder von den Wassermolekülen angestoßen werden. So lassen sich die Eigenschaften der Brown’schen Bewegung erklären; etwa, wie weit sich ein Pollenkorn im Laufe eines gegebenen Zeitintervalls im Mittel von seinem Ausgangspunkt entfernt.
Die folgende schöne (wenn auch visuell etwas anstrengende) Animation aus Wikipedia zeigt, was da passiert; das Pollenkorn ist die größere, gelbe Scheibe, die Moleküle sind die kleineren schwarzen Dinger, die da herumhuschen:

Die Gleichung zur Beschreibung der Bewegung des Pollenkorns ist im Vergleich mit anderen Bewegungsgleichungen der Physik in einer Hinsicht sehr ungewöhnlich. Es ist unmöglich, die Bewegung jedes der Wassermoleküle einzeln als Bahn zu beschreiben. Daher enthält die Gleichung, die Einstein aufstellte, zwar die üblichen Ableitungen für den Ort des Pollenkorns (wie man das von einer Differentialgleichung erwartet), aber zusätzlich noch einen ungewöhnlichen Term: Die Beschreibung des Zufallsprozesses, der wiedergibt, wie die Wassermoleküle mit dem Pollenkorn kollidieren – eine Beschreibung, die diesen Prozess über die Wahrscheinlichkeiten definiert, dass die Kollisionen bestimmte Eigenschaften haben (z.B. bestimmter Impulsübertrag) und die Details (welches individuelle Molekül stößt wann, wie?). Aus heutiger Sicht hatte Einstein die erste stochastische Differentialgleichung aufgeschrieben: eine Gleichung, die Ableitungen der gesuchten Funktion mit (mindestens) einem Zufallsprozess verknüpft.
Die Mathematikerversion der Brown’schen Bewegung
Stochastische Differentialgleichungen sind sonderbar. Der Zufall, der bei solchen Gleichungen hineinspielt, macht selbst solche grundlegenden Eigenschaften der Lösungsfunktionen wie Differenzierbarkeit – sprich: eine vernünftige Definition für die Änderungsraten solcher Funktionen.
Die Brown’sche Bewegung ist ein Beispiel dafür, genauer gesagt, die Mathematiker-Version der Brown’schen Bewegung. Diese ist wie folgt definiert: Könnte man bei der wirklichen, physikalischen Brown’schen Bewegung genau genug hinschauen, dann würde man sehen, dass diese Bewegung auf molekularer Größenskala durch diskrete Stöße zustandekommt; zwischen diesen Stößen bewegt sich das Pollenkorn frei.
Die Mathematiker haben eine eigene Version der Brown’schen Bewegung formuliert, bei der es keine solchermaßen ausgezeichnete Größenskala gibt. Stattdessen bleibt die Zufallsnatur – das charakteristische Verhalten, wie sich das Pollenkorn in einem gegebenen Zeitintervall im Mittel fortbewegt – auf allen Größenskalen erhalten und wird auf all diesen Größenskalen durch eine Gauß-Verteilung beschrieben. (Das ist ein bisschen analog zu der Näherung, Flüssigkeiten als Kontinua zu beschreiben. Im mathematischen Modell bleibt die Flüssigkeit auf beliebig kleinen Größenskalen ein Kontinuum; in [physikalischer] Wirklichkeit stoßen wir ab einer bestimmten, sehr kleinen Größenskala auf die diskreten Atome, aus denen die Flüssigkeit besteht.) Diese mathematische Idealisierung der Brown’schen Bewegung heißt zu Ehren des Mathematikers Norbert Wiener auch Wiener-Prozess.
Die folgende Abbildung zeigt ein Beispiel eines Teilchens, das sich nur in einer einzigen Raumdimension (sprich: entlang einer Linie) bewegt:
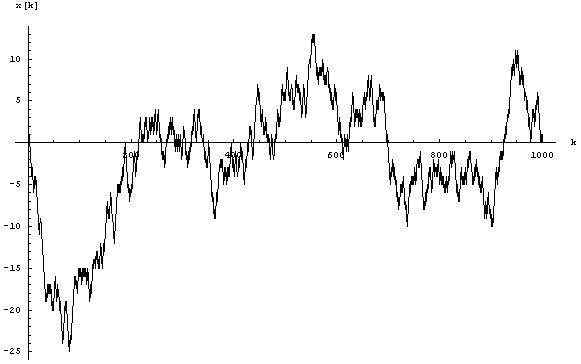
Die x-Achse ist dabei die Zeitachse, während die y-Achse die Richtung beschreibt, in der sich das Teilchen hin oder her bewegen kann. In diesem Beispiel bewegt sich das Teilchen zunächst in die negative y-Richtung, langt etwa bei der Zeit x=200 wieder an seinem Ausgangspunkt an, und so weiter und so fort.
Eine solche Kurve kann direkt immer weiter nach rechts fortgesetzt werden; man lässt das Teilchen immer weiter und weiter laufen. Als Grenzwert kann man die Kurve auf diese Weite unendlich weit nach rechts fortsetzen. Es gibt außerdem eine Möglichkeit, die Kurve nach links fortzusetzen: Man betrachtet einfach eine zweite Brown’sche Kurve, die vom Nullpunkt aus nach rechts in Richtung unendlich läuft, spiegelt diese Kurve an der y-Achse und fügt die beiden Teilkurven zusammen: Fertig ist die zweiseitige Brown’sche Bewegung.
Die Selbstähnlichkeit der Brown’schen Bewegung
Die Brown’sche Bewegung hat eine ziemlich coole Eigenschaft: Wenn man an einer beliebigen Stelle “hineinzoomt” und die Kurve immer genauer betrachtet, dann sieht sie bei jeder Zoomstufe im wesentlichen gleich aus. Allein aus der Art und Weise, wie die Kurve hin und her wandert kann man nicht darauf schließen, bei welcher “Vergrößerung” man die Kurve gerade betrachtet. Diese Eigenschaft heißt Selbstähnlichkeit.
Mathematisch gesehen entspricht das “Hineinzoomen” einer Skalierung in x-Richtung mit dem Faktor cgt;0, und in y-Richtung mit dem Kehrwert der Quadratwurzel aus c. Hier ist eine Animation, wie Hairer sie auch in seinem Vortrag gezeigt hat:
So schön diese Eigenschaft ist, so problematisch ist sie auch. Die Brown’sche Kurve ist nicht glatt, sondern im Gegenteil extrem rauh. Das hat Konsequenzen: Wenn wir die Ableitung einer normalen Kurve an einem gegebenen Punkt bestimmen, dann ist das so etwas ähnliches, wie wenn wir an diesem Punkt immer weiter hineinzoomen – solange, bis die Kurve in unserem Bildausschnitt nicht mehr von einer Gerade zu unterscheiden ist; die Steigung dieser Gerade ist der Wert der Ableitung in diesem Punkt.
Für die Kurve der Brown’schen Bewegung funktioniert dieses Verfahren offenbar nicht: Die Selbstähnlichkeit sorgt dafür, dass wir, egal wie weit wir hineinzoomen, niemals etwas sehen werden, was sich einer Geraden annähert, sondern immer eine Kurve, die der ursprünglichen Kurve ähnelt.
Es ist trotzdem noch möglich, so etwas wie eine Ableitung der Brown’schen Bewegung zu bestimmen. Die, so stellt sich heraus, entspricht weißem Rauschen: einer (ebenfalls extrem rauhen) Kurve, die an jedem Punkt einen zufälligen Wert annimmt, der durch eine Gauß-Verteilung bestimmt wird (je weiter ein Wert von Null abweicht, desto unwahrscheinlicher ist es, dass die Kurve diesen Wert annimmt).
Dieses Ergebnis sollte einen nicht überraschen. In dieser Weise ist die Brown’sche Bewegung schließlich definiert: zufällige Änderung in jedem infinitesimalen Schritt.
Überraschender dürfte sein, dass zwar die Ableitung der Brown’schen Bewegung definiert ist, das Quadrat der Ableitung dagegen nicht: das Quadrat ist unendlich groß!
Exkurs: Per Rechteck zur Unendlichkeit
Wie kann das sein? Bei Zahlen oder herkömmliche Funktionen, kann so etwas nicht vorkommen: Wenn eine Zahl endlich ist, ist es auch ihr Quadrat; für die Werte herkömmlicher Funktionen (bei denen man durch Hineinzoomen an einem Punkt zu einem eindeutigen Funktionswert gelangt) gilt das gleiche. Aber es gibt eine andere etwas ungewöhnliche Funktion, an der man ungefähr verstehen kann, wie so ein ungewöhnliches Verhalten zustandekommt.
[Leser, die wissen, was die Dirac’sche Deltafunktion ist, können sich an dieser Stelle klarmachen, dass das Quadrat der Deltafunktion nicht definiert ist, und zum nächsten Abschnitt springen.]
Angenommen, ich habe eine Rechteckfunktion definiert, die auf einem Intervall von -b/2 bis b/2 den Wert c annimmt und überall sonst Null ist. Ich wähle die Konstanten b und c so, dass bc=1 gilt. Der Graph der Funktion wird so wie in dem folgenden Bild aussehen (Spezialfall b=c=1):
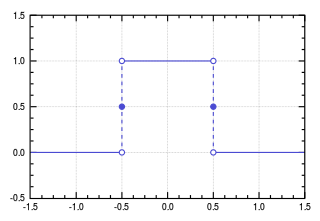
Die Wahl bc=1 bedeutet, dass die Fläche unter der Funktionskurve gleich 1 ist (gemessen wird alles oberhalb der x-Achse).
Jetzt machen wir b>0 immer kleiner. Damit weiterhin bc=1 gilt, müssen wir c immer größer wählen; die Fläche unter der Kurve bleibt bei diesem Vorgehen per Konstruktion immer gleich. Wie sich zeigt, kann man b sogar kontrolliert gegen Null gehen lassen; formal geht c dabei gegen Unendlich. Die Funktion, die dabei entsteht, lässt sich zwar nicht mehr graphisch abbilden, aber sie behält die wichtige Eigenschaft, dass das Integral über sie weiterhin den Wert 1 hat.
Die resultierende (ungewöhnliche) Funktion heißt Dirac’sche Deltafunktion, geschrieben δ(x). Naiv gesehen ist sie nur am Ort x=0 von Null verschieden – und dort ist sie gerade in der geeigneten Weise unendlich, so dass das Integral über δ(x) den Wert 1 ergibt.
Die Funktion δ(x) ist nützlich, weil sie, wenn wir nicht über δ(x) integrieren, sondern über das Produkt f(x)δ(x) mit einer gewöhnlichen (stetigen) Funktion f(x), die folgende Eigenschaft hat: das Integral über dieses Produkt ergibt den Funktionswert von f(x) bei x=0:
Das kann man verstehen, wenn man wieder an die Rechteckfunktion zurückdenkt. Wenn unsere Rechteckfunktion schon sehr dünn und hoch ist, wird f(x) sich über jene Region der x-Achse kaum ändern. (Es sei denn, f(x) ist eine “rauhe” Funktion wie die Brown’sche Bewegung, aber das haben wir ja ausgeschlossen.) Je schmaler wir das Rechteck machen, umso weniger ändert sich f(x). Ist das Rechteck schmal genug, dann machen wir nur noch einen winzigkleinen Fehler, wenn wir f(x) durch f(0) ersetzen – den konstanten Wert f(0) können wir dann aus dem Integral herausziehen; als Integrand verbleibt dann nur noch δ(x), und damit ergibt das verbliebene Integral den Wert 1.
Eine Funktion, die für sich genommen nicht vernünftig definiert ist (wird bei x=0 unendlich!), die aber vernünftig definiert ist, wenn sie irgendwo als Integrand auftaucht, heißt auch Distribution.
Wie sieht es mit dem Quadrat von δ(x) aus?
Naiv gesprochen gilt: Wenn das Integral über das Produkt einer Funktion f(x) mit δ(x) gerade den Wert der Funktion bei x=0 ergibt, dann gilt für das Quadrat von δ(x)
was nun wirklich kein vernünftiges Ergebnis ist.
Da haben wir es, unser Beispiel für eine Funktion – eine Distribution – die vernünftig definiert ist (zumindest solange sie als Integrand auftaucht), aber deren Quadrat nicht vernünftig definiert ist, sondern unendlich ergibt (selbst wenn das Quadrat als Integrand auftaucht).
Zurück zu Brown
Die Situation für das Quadrat der Ableitung der Brown’schen Bewegung ist dieselbe wie die für das Quadrat der Deltafunktion. Wenn man genauer vorgeht, dann sind auch stochastische Differentialgleichungen mithilfe von Integralen definiert – wie bei der Deltafunktion.
Und wie im Falle der Deltafunktion gilt: Wenn etwas als Integrand definiert ist, heißt das noch lange nicht, dass das Quadrat des Objekts auch definiert ist – es kann sogar unendlich sein. Genau das passiert beim Quadrat der Ableitung der Brown’schen Bewegung.
In Teil 2 werden wir eine Anwendung dieser Art von “rauher Kurve” betrachten, zu der Hairer forscht: Grenzflächen zwischen unterschiedlichen Materialien, oder unterschiedlichen Aggregatzuständen (Phasen) desselben Materials.


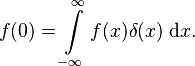
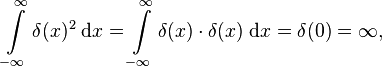
Toll. Selbstähnlichkeit bereits in einem eindimensionalen System und erst noch bei einem System mit praktischer Bedeutung. Dachte immer, man müsse sich einige einfallen lassen um zur Fraktalität zu kommen. Selbstähnlichkeit ist zwar in der Informatik nichts besonders und wird dort mit rekursiven Strukturen in Zusammenhang gebracht, aber wenn man das in der Informatik ansiedelt. siedelt man es im Bereich der diskreten Mathematik an und die Natur ist ja nicht diskret – könnte man meinen.