Astronomisches Grundwissen 9: Kosmische Expansion und Urknall
BLOG: RELATIV EINFACH

Dieser Blogbeitrag ist Teil einer zehnteiligen Serie, die astronomisches Grundwissen vermitteln soll. Alle Beiträge auf einen Blick:
- Nachthimmel, Lichtverschmutzung, Beobachtungen
- Bilder, Spektren, Einfluss der Atmosphäre, Entfernungen
- Unser Sonnensystem
- Die Sonne und andere Sterne
- Das Leben der Sterne
- Exoplaneten
- Die Milchstraße und andere Galaxien
- Kosmische Strahlung, Gravitationslinsen, großräumige Struktur
- Kosmische Expansion und Urknall
- Galaxienentwicklung, Dunkle Energie und Ausblick
Näheres zur Motivation der Serie und dazu, was ich unter astronomischem Grundwissen verstehe, findet sich hier in Teil 1.
Kosmische Expansion
Mit Hilfe des Dopplereffekts, den ich in Teil II bereits im Zusammenhang mit den Exoplaneten geschilderten hatte, lässt sich vergleichsweise einfach nachweisen, ob und wie schnell die Entfernung einer Galaxie zu uns zu- oder abnimmt. Man muss dazu lediglich messen, ob die Linien im Spektrum der Galaxie in Richtung rotes oder blaues Ende des Spektrums verschoben sind (“Rotverschiebung” oder “Blauverschiebung”).
Den Bewegungen der Galaxien in Haufen und Superhaufen nach würde man erwarten, dass sich bei solchen Messungen ein einheitliches Bild ergibt. Wir sollten messen, dass sich alle Galaxien mit höchstens einigen tausend Kilometern pro Sekunde auf uns zu oder von uns weg bewegen, bunt gemischt – und unabhängig davon, wie weit sie von uns entfernt sind.
Was solche Messungen stattdessen zeigen ist, dass sich Galaxien bevorzugt, ab einer bestimmten Entfernung sogar ausschließlich von uns fortbewegen, genauer: dass ihr Spektrum eine Rotverschiebung zeigt. Dabei gibt es eine auffällige Systematik: Je weiter eine Galaxie von uns entfernt ist, umso größer ist die Rotverschiebung.
Die einfachste und heute unter den Astronomen allgemein akzeptierte Erklärung für diese Systematik ist, dass der Kosmos expandiert. Damit ist gemeint: Auf galaktischen Größenskalen nehmen die Entfernungen zwischen allen Galaxien in gleicher Weise zu, nämlich um jeweils den gleichen Faktor, etwa so, als würde zwischen ihnen immer mehr Raum “entstehen”. Ein schematisches Beispiel zeigt die folgende Animation (Animation: AEI/Einstein Online), in der alle Abstände zwischen den gezeigten Galaxien in dem dargestellten Zeitraum um den Faktor 2 zunehmen:

Zu Modellvorstellungen wie Gummiband oder Rosinenkuchen, mit denen man sich die Expansion veranschaulichen kann, hatte ich hier bereits vor einiger Zeit etwas geschrieben.
Im Rahmen der Allgemeinen Relativitätstheorie lassen sich Modelluniversen, in denen genau solch eine Expansion auftritt, präzise beschreiben – ja, es ist im Rahmen dieser Theorie so gut wie unmöglich, ein Universum zu finden, das nicht expandiert oder, umgekehrt, in sich zusammenstürzt! Systematische Messungen der Rotverschiebungen und der Häufigkeitsverteilung der Objekte bei unterschiedlichen Entfernungen liefern wichtige Hinweise auf die Richtigkeit solcher expandierenden Modelle.
Die Rotverschiebung selbst erweist sich in solchen Modellen übrigens gerade nicht als ganz normaler Dopplereffekt für Galaxien, die sich durch den Raum bewegen. Sie entsteht stattdessen, weil das Licht ferner Galaxien auf dem Weg zu uns durch die Expansion des Kosmos gestreckt wird. Dass seine Wellenlänge durch die Streckung immer größer wird entspricht einer Rotverschiebung, die ob ihres Ursprungs kosmologische Rotverschiebung genannt wird.
Wichtig ist noch zu wissen, wie die Expansion gebundene Systeme beeinflusst – eine Galaxie beispielsweise, deren Sterne durch gegenseitige Schwerkraft aneinander gebunden sind, unser Sonnensystem, oder auch die Atome, aus denen wir bestehen, mit ihren Atomkernen und daran gebundenen Elektronen. Die kurze Antwort ist: gar nicht. Ist die Bindung stark genug, so wird sie durch die kosmische Expansion nicht verändert. Erst ab den Längenskalen, auf denen der Kosmos im Durchschnitt in etwa überall die gleiche Dichte hat – also keine größeren Massenkonzentrationen hie und -defizite da – kann die kosmische Expansion ungehindert wirken.
Die Urknallphase
Wenn das Universum expandiert, dann waren sich im Umkehrschluss alle Objekte darin in der Vergangenheit näher als heute. In den modernen kosmologischen Modellen lässt sich die Expansion sogar in eine Phase in der Vergangenheit extrapolieren, in der die gesamte Materie des heute von uns beobachtbaren Universums auf engstem Raum komprimiert und der gesamte Kosmos mit einem extrem dichten, extrem heißen Gemisch aus Elementarteilchen gefüllt war. Das war die sogenannte Urknallphase, aus der der Kosmos, den wir um uns herum sehen, vor rund 13,8 Milliarden Jahren hervorgegangen ist.
Tatsächlich kann man die Geschichte des Kosmos in den Modellen soweit zurückverfolgen, dass die gesamte Materie des beobachtbaren Universums auf einen einzigen Punkt zusammengepresst war, mit entsprechend unendlich hoher Dichte. Diese sogenannte Urknallsingularität ist ein deutliches Zeichen, dass unsere Modelle an dieser Stelle an ihre Grenzen stoßen. Warum das so ist, ist nicht überraschend. Aus der Physik wissen wir, dass bei mikroskopischen Größenskalen sogenannte Quanteneffekte wichtig werden, wie sie Physiker im Rahmen der Quantentheorien beschreiben – Beispiele sind die Quantenmechanik samt ihrer Anwendung auf die Atomphysik oder Quantenfeldtheorien zur Beschreibung der Eigenschaften von Elementarteilchen.
Dass nahe der Urknallsingularität riesige Massen mikroskopisch klein zusammengepresst sind, zeigt, dass wir diese Situation eigentlich mit einer Theorie der Quantengravitation beschreiben müssten, die einerseits die Physik der Allgemeinen Relativitätstheorie, andererseits die der Quantentheorie umfasst. Allerdings haben die Physiker bislang keine vollständige Quantengravitationstheorie formulieren können – obwohl sie es seit mehr als 60 Jahren versuchen, und obwohl es einige interessante Kandidaten wie Stringtheorie oder Schleifen-Quantengravitation gibt.
Über die frühesten Urknallphasen und insbesondere die Urknallsingularität selbst lassen sich deswegen derzeit noch keine gesicherten Aussagen treffen. Wir wissen schlicht nicht, was da los war und ob das Universum tatsächlich einen so abrupten Anfang hatte, wie die klassischen (d.h. die Quantengravitation vernachlässigenden) Modelle behaupten. Bereits Sekundenbruchteile nach der Urknallsingularität funktionieren diese herkömmlichen Modelle dagegen durchaus. Für eine Angabe wie “200 Millionen Jahre nach dem Urknall” macht es daher keinen Unterschied, ob mit “Urknall” tatsächlich die Urknallsingularität oder die frühen, auch ohne Quantengravitation gut beschreibbaren Zeitpunkte der Urknallphase gemeint sind. (Zur Unterscheidung von Urknallsingularität und Urknallphase siehe auch hier.)
Die Frühgeschichte des Kosmos
Je näher man an die Urknallsingularität zurückgeht, umso unsicherer wird unser Wissen. Um 10-43 Sekunden nach dem Urknall herum sind wir direkt in der Quantengravitationsphase: Hier gilt: Nichts Genaues weiß man nicht. Bei ungefähr 10−37 Sekunden folgte vermutlich eine sogenannte Inflationsphase, in der sich das Universum (exponentiell) beschleunigt ausdehnt. Diese Phase wird benötigt, um eine Reihe von Eigenschaften des Kosmos zu erklären: seine weitgehende Homogenität; die tatsächlich beobachtete Raumgeometrie, die den Regeln der aus der Schule bekannten Euklidischen Geometrie folgt, sowie die Abwesenheit bestimmter exotischer Teilchen.
Je weiter die Expansion fortschritt, desto mehr kühlte die im Kosmos erhaltene Materie ab und desto geringer wurde ihre Dichte. Im Laufe der Zeit machte das Teilchengemisch, welches das Universum ausfüllte, der immer geringeren Dichte und Temperatur entsprechend eine Reihe von Veränderungen durch: Die grundlegenden Kräfte nahmen ihre heutigen Formen an (starke Kernkraft, schwache Kernkraft, Elektromagnetismus); Quarks fanden sich zu Teilchen wie Protonen und Neutronen zusammen; Materie und Antimaterie vernichteten sich gegenseitig, bis nur noch ein Rest Materie und viel Strahlung übrig waren. Aus Protonen und Neutronen entstanden in den ersten Minuten der Urknallphase leichte Elemente wie schwerer Wasserstoff (ein Proton, ein Neutron), Helium-3 (2 p, 1 n), Helium-4 (2 p, 2n) und Lithium-7 (3 p, 4 n). Der Vergleich der dazu vorhergesagten Häufigkeiten für diese Elemente mit Rekonstruktionen der ursprünglichen Elementhäufigkeiten aus der Beobachtung möglichst urtümlicher Sterne ist ein weiterer erfolgreicher Test, den die Urknallmodelle bestanden haben.
Die kosmische Hintergrundstrahlung
Rund 380.000 Jahre nach dem Urknall kam es zu einer wichtigen Veränderung. Vorher war das Weltall mit geladenen Teilchen angefüllt; es war damit komplett undurchsichtig: Lichtteilchen wurden immer wieder und wieder abgelenkt und hatten so keine Möglichkeit, Informationen über fernere Himmelsregionen zu übermitteln. Jetzt war die Temperatur des Kosmos soweit gefallen, dass sich aus den herumschwirrenden Atomkernen und Elektronen elektrisch neutrale Atome bilden konnten, ohne von der heißen Wärmestrahlung sofort wieder auseinandergerissen zu werden. Das Ergebnis: Das Weltall wurde auf einmal durchsichtig. Ab diesem Zeitpunkt konnte sich Licht weitgehend unbeeinflusst fortbewegen. Das heißt nicht, dass man damals viel hätte erkennen können – der Kosmos war immer noch mit hell gleißender Wärmestrahlung angefüllt. Aber es hatte eine wichtige Konsequenz.
Wie anfangs erwähnt: Wenn die Astronomen in die Ferne sehen, schauen sie immer auch in die Vergangenheit. Außerdem gilt aber, wie im Alltag auch: In jede Richtung können wir nur soweit sehen, bis unser Blick auf etwas Undurchsichtiges trifft. Wenn wir in die Ferne und damit in die Vergangenheit sehen, gilt aber: Überall dort, wo unser Blick nicht auf einen Stern, eine Galaxie oder sonst ein Himmelsobjekt trifft, wird unser Blick trotzdem auf etwas Undurchsichtiges treffen, nämlich dann, wenn die Entfernung so groß ist, dass wir das Universum so sehen, wie es in der Urknallphase war – nämlich undurchsichtig. Anders ausgedrückt: Von überall am Himmel erreicht uns die Strahlung, die 380.000 Jahre nach dem Urknall freigesetzt wurde, als das Universum durchsichtig wurde. Das ist die sogenannte kosmische Hintergrundstrahlung, oft auch als “Echo der Urknalls” oder Ähnliches bezeichnet.
Die Hintergrundstrahlung ist heute längst nicht mehr so gleißend hell wie damals. Zusammen mit dem Universum hat sie sich ausgedehnt, ist immer weiter verdünnt und zudem wie alles andere Licht aus der Ferne rotverschoben worden. Derzeit liegt ihr Maximum längst nicht mehr im Bereich des sichtbaren Lichts, sondern im Bereich der für unsere Augen unsichtbaren Mikrowellenstrahlung.
Die kosmische Hintergrundstrahlung ist eine Wärmestrahlung, wie sie ein idealer (“schwarzer”) Körper mit einer Temperatur von 2,73 Kelvin, also 2,73 Grad Celsius über dem absoluten Nullpunkt abgeben würde. Sie erreicht uns aus allen Himmelsrichtungen; dementsprechend wird sie oft ähnlich einer Weltkarte dargestellt wie in diesem Bild des US-amerikanischen Satelliten WMAP, der die Hintergrundstrahlung über insgesamt neun Jahre hinweg vermessen hat (Bild: NASA/WMAP Science Team):
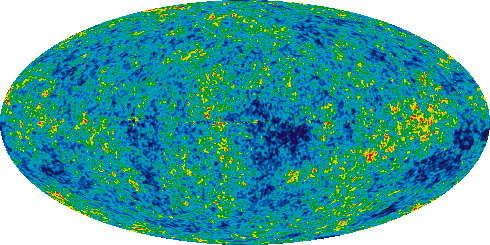
Dargestellt ist in diesem Falschfarbenbild, wie weit die aus der Hintergrundstrahlung erschlossene Temperatur variiert – eine rot dargestellte Himmelsregion ist um einige zehntausendstel Grad wärmer als der Durchschnitt, eine dunkelblau dargestellte um einige zehntausendstel Grad kälter.
Die kosmische Hintergrundstrahlung enthält reichhaltige Informationen über das früheste Universum. Die winzigen Temperaturfluktuationen zeigen, wie sich Materie schon sehr früh unter der eigenen Schwerkraft ein wenig verklumpte, und auch, dass es damals Dunkle Materie gegeben haben muss, die nicht elektromagnetisch miteinander wechselwirkte – und zwar soviel Dunkle Materie, wie sich auch aus den schon erwähnten unabhängigen Abschätzungen (Rotation von Galaxien; Galaxienbewegungen in Haufen) ergibt.
Über die genaue Struktur der Temperaturfluktuationen (wie groß sind die Fluktuationen zwischen nahe beieinanderliegenden Regionen? Wie groß sind sie bei welchen größeren Abständen?) treffen die kosmologische Modelle ganz spezifische Aussagen; der Vergleich mit den Beobachtungsdaten stellt einerseits einen ziemlich strengen Test dieser Modelle dar und ermöglicht zum anderen die Bestimmung grundlegender Parameter wie das Alter des Universums und die großräumigen geometrischen Eigenschaften des Kosmos.
Auch erste direkte Hinweise auf die oben erwähnte Inflationsphase finden sich dort; genauere Messungen mit dem ESA-Satelliten Planck, die derzeit analysiert werden, sollen belastbare Aussagen dazu treffen, was es mit der Inflationsphase auf sich hatte.
Wie in Teil 8 bereits beschrieben: Die kosmische Hintergrundstrahlung sollte nicht verwechselt werden mit der kosmischen Strahlung, also der Teilchenstrahlung, die uns aus dem All erreicht!
Rotverschiebung als Entfernungs- und Zeitmaß
Bevor es mit der kosmischen Geschichte weitergeht, hier noch ein wichtiges Werkzeug: Ich hatte bereits erzählt, dass es in einem expandierenden Universum einen direkten Zusammenhang zwischen der Entfernung einer fernen Galaxie und der Rotverschiebung gibt, die wir für sie messen.
Tatsächlich ist die Situation noch komplizierter. Es ist in einem expandierenden Kosmos gar nicht mehr eindeutig, was mit dem Begriff der Entfernung z.B. zu einer fernen Galaxie überhaupt gemeint ist. Die Entfernung zu jenem Zeitpunkt als das Licht der Galaxie, das uns jetzt erreicht, ausgesandt wurde? Die viel größere Entfernung jetzt? Die Zeit, die das Licht der Galaxie für seine Reise zu uns benötigt hat, malgenommen mit der Lichtgeschwindigkeit? Auch daraus, wie lichtschwach uns ein Objekt gegebener Leuchtkraft erscheint, oder wie klein ein Objekt gegebener Größe, folgt eine Entfernung – sind diese Entfernungsbegriffe gemeint? In einem expandierenden Universum weichen all diese Entfernungsbegriffe bei sehr fernen Objekten voneinander ab.
Die Rotverschiebung hat den Vorteil, sehr leicht messbar zu sein – auch für viele Objekte, deren Entfernung wir auf andere Weise nicht bestimmen können. Hat man die Eigenschaften des kosmologischen Modells (im wesentlichen: das Gesamtalter des Universums und die geometrischen Eigenschaften des Raums) einmal bestimmt, kann man die Rotverschiebung, die in der Regel mit dem Buchstaben z bezeichnet wird, in die anderen Entfernungsmaße umrechnen. Dabei hilft z.B. Ned Wright’s Cosmology Calculator (“age at redshift” ist das Alter des Universums, als das betreffende Licht ausgesandt wurde; “light travel time” die Lichtlaufzeit, “comoving radial distance” der heutige Abstand des Objekts von uns, “angular size distance” die Entfernung, die man aus der scheinbaren Größe und “luminosity distance” die Entfernung, die man aus der Helligkeit des Objekts erschließen würde. In der linken Spalte lassen sich die kosmologischen Parameter eingeben; wer dort einfach auf “general” klickt, started die Rechnung mit den heute akzeptierten Standardwerten).
Unter sich reden extragalaktische Astronomen üblicherweise direkt von der Rotverschiebung z, wenn sie Informationen zum Abstand z.B. einer fernen Galaxie geben wollen. Das z ist definiert als die relative Änderung der Wellenlänge, die das betreffende Licht erfahren hat (also z gleich Wellenlängenänderung geteilt durch Wellenlänge). Eine Rotverschiebung z heißt, dass zu jener Zeit, als das betreffende Licht ausgesandt wurde, alle Galaxien im Universum um den Faktor 1/(1+z) näher beisammen hockten.
Kosmische Geschichte
Die Geschichte des Kosmos nach Freisetzung der kosmischen Hintergrundstrahlung (bei der Rotverschiebung z = 1100) ist zum einen die Geschichte der immer weiter fortschreitenden Verklumpung der anfangs noch recht homogenen Dunklen Materie. Aus den winzigen Temperaturfluktuationen der kosmischen Hintergrundstrahlung lässt sich erschließen, welche winzigen Dichtefluktuationen es direkt bei Freisetzung der Hintergrundstrahlung gegeben haben müsste – mit anderen Worten: Wie viele wie große Zonen etwas geringerer und etwas höherer Dichte es im frühen Universum gegeben hat.
Mit dieser Information wiederum kann man simulieren, was dann passiert: wie die etwas dichteren Regionen aufgrund ihrer höheren Schwerkraft noch weitere Materie zu sich heranziehen, so dass sich die Schwerkraft noch weiter erhöht, und so weiter. Die Simulationen, hier ein Beispiel aus der Gruppe um Andrey Kravtsov, zeigen, was dann passiert:
Aus dem zunächst nahezu perfekt homogenen Universum wird ein Gebilde aus Filamenten und Knoten – entsprechend der großräumigen Verteilung von Galaxienhaufen, die tatsächlich beobachtet wird. (Die Expansion des Universums wird in dieser Visualisierung nicht mit dargestellt, um die Verklumpung des Universums deutlich zeigen zu können.)
Bei dieser großräumigen Verklumpung hat die herkömmliche Materie wenig Einfluss. Was sich entlang des “Skeletts” aus Dunkler Materie tut, ist aber nicht minder interessant. Innerhalb der ersten paar hundert Millionen Jahre entstehen die ersten Sterne – wie erwähnt sind sie besonders massereich; solche massereichen Sterne leuchten extrem stark und sind darum schon nach wenigen Millionen Jahren ausgebrannt. Zusammen mit frühen Quasaren (siehe oben) – wer da in welchem Maße beiträgt ist freilich noch nicht geklärt – ionisieren den Wasserstoff im frühen Universum, das dadurch für das Ultraviolettlicht der Sterne durchsichtig wird.
Weiter geht es mit Teil 10: Galaxienentwicklung, Dunkle Energie, Ausblick
Ich danke meinen Kollegen Knud Jahnke, Carolin Liefke und Jakob Staude für hilfreiche Anmerkungen zu diesem Text.


bckground radiation: non stellar photons
Die Mikrowellenhintergrundstrahlung geht ja auf ein Ereignis zurück, welches nur einige tausend Jahre in Anspruch nahm, nämlich das Transparentwerden des Universums für Photonen. Diese konnten sich nach der Bildung von neutralen Atomen aus dem vorher bestehenden Gemisch von freien Atomkernen und freien Elektronen plötzlich geradlinig bewegen. Und das taten sie dann auch und tun es immer noch. Doch diese Mikrowellenstrahlung ist letztlich nur darum abgrenzbar von anderer stellarer Strahlung weil sie
1) nicht stellaren Ursprungs ist und ihre Quellen uniform verteilt sind über das ganze Raumgebiet des damaligen Universums
2) Die Sterne erst sehr viel später entstanden als der Ursrpungszeitpunkt der Mikrowellenstrahlung, welche 377’000 Jahre nach dem Urknall entstand. Zwischen dem Enstehen der Mikrowellenstrahlung und dem Entstehen der ersten Sterne gab es noch das dunkle Zeitalter.
Eigentlich sollte das Licht der allerersten Sterne aufgrund der Rotverschiebung (Streckung durch den expandierenden Raum) auch im Mikrowellenbereich liegen, wenn auch aufgrund der späteren Emissionszeit etwas kürzerwellig als die Hintergrundstrahlung. Zusätzlich ist dieses stellare Licht aber nicht-thermischen Ursprungs wie es das die Hintergrundsstrahlung ist. Somit sollte es eine andere spektrale Verteilung haben.
Das sind so die Gedanken, die mir zum obigen Artikel kommen.
Geometrie
Vielen Dank für diese Ausführungen.
Was ich in Zusammenhang mit dem Urknall nie verstanden habe, ist die Frage der Geometrie des Universums, also ob es unendlich ist und wie viele Dimensionen es hat.
Wenn man einen Raum unendlichen Volumens annimmt, dann kann man sich eine Ausdehnung bzw. Dichteabnahme darin vorstellen und umgekehrt eine Dichtezunahme gegen Unendlich an einem Zeitpunkt in der Vergangenheit, es kann dann aber nie eine Konzentration „in einem Punkt” gegeben haben, da man ein unendliches Volumen nicht in eine endliche Distanz pressen kann, es bleibt immer unendlich, nur die Dichte ändert sich.
Für den Kollaps in einen Punkt müsste die Geometrie doch geschlossen sein, also wie der Oberfläche einer Kugel oder einer Kreislinie analog ein Volumen in sich zurücklaufend, zwar ohne Grenze/Kante aber mit einem endlichen Inhalt und messbarem Durchmesser.
Nur ein solch endlicher Inhalt liesse sich theoretisch in einen Punkt komprimieren, analog zur gravitativen Raumkrümmung in einer vierten Dimension könnte man sich eine Hypersphäre oder einen 3-Torus vorstellen, aber es wäre immer eine geschlossene Geometrie, egal mit wie vielen Dimensionen.
Ich lese immer, die gemessene beschleunigte Expansion des Universums lege eine offene Geometrie nahe und verstehe nicht, wie etwas nicht Eingerolltes, sich jetzt und früher in die Unendlichkeit Erstreckendes jemals in einem (nulldimensionalen) Punkt eingeschlossen gedacht werden kann.
Wo mache ich da den/die Denkfehler?
Volumen
Wenn ich das Urknallmodell richtig verstanden habe, expandiert das Universum nicht in den uns bekannten Raum sondern “unsere” Raumzeit ensteht erst mit dem Urknall. Erst durch die Expansion entsteht so etwas wie Volumen, das somit auch nicht unendlich ist und letztlich auch nichts Unendliches “in einen mathematischen Punkt gepresst” werden müsste, wenn man sich Richtung Urknall zurückdenkt. Vielleicht löst das Ihr Dilemma.
mfG
Mythos Urknall
Der “Urknall” ist lediglich ein Entstehungsmythos.
Sowohl die Elementarteilchenphysiker als auch die Astrophysiker haben sich Wolkenkuckucksheime aufgebaut.
Joachim Datko – Physiker, Philosoph
oder viel einfacher,
nämlich ohne gegenteilige Evidenzen einfach nur im Gefolge von “Durchknall und Holzweg” dahergeschrieben. Meckern alleine macht noch keinen Physiker.
@Heinz Gerd / Geometrie
»Was ich in Zusammenhang mit dem Urknall nie verstanden habe, ist die Frage der Geometrie des Universums, also ob es unendlich ist und wie viele Dimensionen es hat.«
Die “Urknallsingularität” in den kosmologischen Friedman Modellen ist kein dimensionsloser Punkt, sondern als Punktmenge entspricht sie einem 3-Raum von der gleichen Beschaffenheit wie zu jedem regulären Moment kosmologischer Zeit. Lasst man die kosmologische Zeit rückwarts laufen, dann kollabiert bei Annäherung an die Singularität nicht der 3-Raum auf einen Punkt, sondern die durch die Modelle vorgegebene Art und Weise räumlicher Abstandsmessung degeneriert in dem Sinne, dass je zwei Punkte schlussendlich den Abstand null voneinender haben müssten.
Bezeichnenderweise schrieb Friedman in seiner Pionierabeit von 1922, “Über die Krümmung des Raumes”, auch kein Wort von Expansion. Die hat erst Lemaître da hineingedeutet. Mit dem explosiven “Wooom!!!”, das in pop.-wissenschaftl. Animationsfilmchen typischerweise einen “Urknall” begleitet, wird man jedenfalls nur auf den Holzweg geschickt.
… aber nicht komplizierter als nötig.
Markus Pössel schrieb (10. März 2013, 20:30):
> Tatsächlich ist die Situation noch komplizierter. Es ist in einem expandierenden Kosmos gar nicht mehr eindeutig, was mit dem Begriff der Entfernung z.B. zu einer fernen Galaxie überhaupt gemeint ist.
Was wäre überhaupt mit “expandierend” gemeint, wenn für eine entsprechende Definition nicht zunächst ein eindeutiger Begriff von “Entfernung” zur Verfügung stünde?
> Die Entfernung
… die — Was? (Wie misst man das denn, zumindest im Prinzip?) …
> zu jenem Zeitpunkt als das Licht der Galaxie, das uns jetzt erreicht, ausgesandt wurde?
Erlaubt die zugrundeliegende Messdefinition denn überhaupt die Einschränkung auf einen bestimmten “Zeitpunkt als“?
> Die viel größere Entfernung jetzt?
Ist die Messgröße “Entfernung” etwa gar nicht kompatibel mit dem Zustand des betrachteten Paares von Beteiligten (d.h. von “uns” und “der Galaxie, deren Licht uns jetzt erreicht“)?
Geht es vielleicht eher um den Vergleich der (konstanten) “Entfernung” zwischen “uns” und jemand Geeignetem, der die zu betrachtende “Galaxie” traf, “als das Licht der Galaxie, das uns jetzt erreicht, ausgesandt wurde” mit der (konstanten) “Entfernung” zwischen dieser “Galaxie” und jemand Geeignetem, der “uns jetzt” traf?
> Die Zeit, die das Licht der Galaxie für seine Reise zu uns benötigt hat,
Also der “s”-Wert Null?
(Oder ansonsten: wessen Dauer?, zwischen welchen beiden Anzeigen?)
> malgenommen mit der Lichtgeschwindigkeit?
> Auch daraus, wie lichtschwach uns ein Objekt gegebener Leuchtkraft erscheint
Was bedeutet/wie misst man das Verhältnis zwischen “gegebener Leuchtkraft” und
“lichtschwacher Erscheinung“?; insbesondere sofern für eine entsprechende Definition nicht zunächst ein eindeutiger Begriff von “Entfernung” zur Verfügung stünde.
> oder wie klein ein Objekt gegebener Größe, […]
… gegebener — Was?.
@Chrys
„…dann kollabiert bei Annäherung an die Singularität nicht der 3-Raum auf einen Punkt, sondern die durch die Modelle vorgegebene Art und Weise räumlicher Abstandsmessung degeneriert in dem Sinne, dass je zwei Punkte schlussendlich den Abstand null voneinender haben müssten.”
Danke, das leuchtet mir ein.
@Martin Holzherr
Die ersten Sterne könnte man hier in der Tat noch einbauen. Bei Rotverschiebungen von z=20-80 sind die gute Ziele für ALMA, die ja, wie’s der Zufall will, heute eingeweiht wird.
@Frank Wappler
Die Kosmologen kennen viele Entfernungsbegriffe. Mehr dazu mag der Physiker (allerdings auch der Nichtphysiker) im Kosmologie Tutorial von Ned Wright erfahren, den Markus Pössel u.a. oben im Text verlinkt hat.
Für John Synge ergibt sich physikalisch immerhin ein Sinn, wenn die universelle Expansion auf luminosity distance bezogen wird. Ausführlich in seinem GR Buch, Ch. VIII, §3.
Die meisten Kosmologen empfinden da ganz bestimmt weniger relativistische Skrupel als Synge. Es ist gewiss nicht so verkehrt, wenn Wert auf die Feststellung gelegt wird, dass die Sache mit der Expansion doch irgendwie subtiler ist, als es sich mit Luftballons und Rosinenbrot im Kindergarten vermitteln lässt. Die üblichen Popularisierungen verwenden alle eine feste Hintergrundmetrik, relativ zu der sich dann irgendwas anschaulich ausdehnt. Und genau so etwas liefern die kosmologischen Modell-Raumzeiten gerade nicht.
So gewissenhaft wie vorstellbar
Chrys schrieb (14.03.2013, 12:20):
> Die Kosmologen kennen viele Entfernungsbegriffe.
Ob sich darunter wohl zumindest ein “Entfernungs“-Begriff befindet, der dahingehend nachvollziehbar ist (bzw. “anschlussfähig”, nicht wahr? &), dass seine Definition nicht wiederum einen (anderen) “Entfernungs“-Begriff erfordert und voraussetzt ??
> Mehr dazu mag der Physiker (allerdings auch der Nichtphysiker) im Kosmologie Tutorial von Ned Wright erfahren, den Markus Pössel u.a. oben im Text verlinkt hat.
Eine Quelle, bei der öffentliche Nachfrage bzw. Rückmeldung offenbar überhaupt nicht vorgesehen ist !??
Da lob ich mir aber Markus Pössels SciLog! (Siehe entsprechende Nachfragen/Rückmeldungen z.B. in meinem vorausgegangenen Kommentar in diesem SciLog, 12.03.2013, 16:32.)
> Für John Synge ergibt sich physikalisch immerhin ein Sinn, wenn die universelle Expansion auf luminosity distance bezogen wird. Ausführlich in seinem GR Buch, Ch. VIII, §3.
(Von Synges Buch habe ich leider nur das Kapitel zum “five point curvature meter” parat. Und selbst davon nur diejenigen Auszüge, die von keinem der Beteiligten mehr erfordern als die Reihenfolge oder Koinzidenz seiner eigenen Beobachtungen zu beurteilen; ohne dass man von vornherein wissen und einig sein müsste, welche Uhren “gut” bzw. welche Pendelschläge “gleich” sind.)
Versuch doch bitte mal zu erklären, was (meinentwegen nach Synge) “luminosity” bedeuten soll, ohne dabei irgendeinen “Entfernungs“-Begriff zu benutzen und vorauszusetzen.
> […] Wert auf die Feststellung gelegt wird, dass die Sache mit der Expansion doch irgendwie subtiler ist, als es sich mit Luftballons und Rosinenbrot im Kindergarten vermitteln lässt
Vermitteln mit … Was??
@Frank Wappler
Laienhaft ausgedrückt, luminosity distance wird definiert als diejenige Grösse, die formal den Unterschied macht zwischen absoluter und scheinbarer Helligkeit leuchtender Objekte. Und diese astronomischen Helligkeiten sind als Observable unabhängig von jeglichem Distanzbegriff.
Im übrigen hat Synge diese Sache nicht allein ausgeheckt. Vielmehr verweist er dabei auf ein Paper von Edmund Whittaker, das hier zu haben ist:
http://adsabs.harvard.edu/abs/1931RSPSA.133…93W
Dazu sei allerdings noch bemerkt, dass Whittakers Definition kritisiert worden war, und zwar hier (leider nicht frei):
http://dx.doi.org/10.1007/s10714-007-0447-x
Der etwas spezielle Fall konform flacher Raumzeiten, wie er von Synge betrachtet wird, scheint davon jedoch nicht tangiert. Andernfalls hätte Synge sicherlich konkret auch Etherington genannt, dessen Arbeit er ohnehin in seine Bibliographie aufgenommen hat.
The brightest knife in the barrel?
Chrys schrieb (17.03.2013, 18:35):
> […] zwischen absoluter und scheinbarer Helligkeit leuchtender Objekte. Und diese astronomischen Helligkeiten sind als Observable unabhängig von jeglichem Distanzbegriff.
Falls sowohl “absolute Helligkeit” als auch “(astronomische) scheinbare Helligkeit” als Observable gänzlich unabhängig von jeglichem Distanzbegriff wären (mal ganz abgesehen vom Begriff “luminosity distance” an sich), dann gäbe es doch kaum die “reciprocity relation”, die in http://en.wikipedia.org/wiki/Luminosity_distance offenbar im Zusammehang mit I.M.H. Etherington genannt wird — oder?
p.s.
> […] ein Paper von Edmund Whittaker, das hier zu haben ist:
> […] Dazu sei allerdings noch bemerkt, dass Whittakers Definition kritisiert worden war, und zwar hier (leider nicht frei):
Zunächst mal Dank und Anerkennung für die gewohnt sachdienliche Recherche.
Ich stelle fest, dass die erste Seite beider dieser Artikel ohne Weiteres einsehbar ist. Für alles weitere des ersten Artikels ist (wenigstens) persönliche Registrierung erforderlich (vielleicht mache ich das noch); an den weiteren Inhalt des zweiten komme ich ohne Weiteres leider überhaupt nicht heran.
Die könnten nämlich auch interessant für ein Problem sein, dass mich noch eher interessiert (und das auch schon berührt wurde, als man die Grundlagen von “Grundwissen” noch ernstnahm):
Gegeben drei verschiedene Ereignisse, “£”, “¥” und “€”, die paarweise zueinander gleichermaßen “lichtartig” sind, und gegeben weitere geeignete Ereignisse, soweit erforderlich, lassen sich die drei entsprechenden (geordneten) Ereignispaare “{ £, ¥ }”, “{ £, € }” und “{ ¥, € }” darüberhinaus quantitativ vergleichen bzw. unterscheiden?
@Frank Wappler
Das Whittaker Paper kann ich offenbar von adsabs über den DOI Link problemlos bekommen. Keine Ahnung woran es liegt, falls es da Schwierigkeiten hat.
Das Besondere bei Etherington ist, dass er ein allg. Reciprozitätstheorem gezeigt hat, das insbesondere auch für inhomogene und anisotrope Modelluniversen anwendbar ist. Synge hat sich in seinem Buch auf den konform flachen Fall beschränkt, der u.a. die Raumzeiten von de Sitter und Friedman umfasst. Und dazu reicht ihm der Whittaker hin.
Allfällige Fragen zur Bestimmung astronomischer Helligkeiten delegiere ich mit Freuden an die lokalen SciLogs Astro-Experten 🙂
Infinitesimal-fest
Chrys schrieb (19.03.2013, 11:42):
> Das Whittaker Paper kann ich offenbar von adsabs über den DOI Link problemlos bekommen.
Überraschung — dahinter steckt der Artikel ja!
(Ich glaube, du hast in sciLog-Kommentaren schon öfter Referenzen per “adsabs” angegeben, die ich bisher per “Electronic Refereed Journal Article (HTML)”-Link finden konnte.
Also, danke, wieder was gelernt!)
E.T. Whittaker schrieb (Proc. R. Soc. Lond. A 133 (821), 93, 1931):
>
Ja, daran wäre jedenfalls der anscheinend undefinierte Begriff “near” zu kritisieren
bzw. nachzufragen; und natürlich auch der ganz offensichtlich undefinierte Begriff ““instantaneous three dimensional space´´“.
Da wünsche ich mir doch sehr, die oben erwähnte Kritik von Etherington insbesondere daraufhin ansehen zu können! …
> Das Besondere bei Etherington ist, dass er ein allg. Reciprozitätstheorem gezeigt hat, das insbesondere auch für inhomogene und anisotrope Modelluniversen anwendbar ist.
Excellent use of “Modell” in a SciLogs comment!
> Allfällige Fragen zur Bestimmung astronomischer Helligkeiten delegiere ich mit Freuden an die lokalen SciLogs Astro-Experten
Mir sollen jegliche Antworten dazu willkommen sein, solang sie nur nachvollziehbar wären;
also Modell-unabhängig und insbesondere ohne irgendwelche Annahmen oder Vorgaben hinsichtlich “Distanz”.
(Ob ausgerechnet Astro-Experten dazu imstande sind? Mal überraschen lassen … 😉