Gute Maßeinheiten: Hintergrundseite
BLOG: RELATIV EINFACH

Dies ist die Hintergrundseite zum Blogeintrag Was ist eine gute Maßeinheit? Wie dort beschrieben, hat die Seite mehrere Funktionen: Sie versammelt etwaige neue Textteile, in denen Aussagen aus dem Haupttext genauer erklärt werden, sie zeigt die ursprüngliche Version des Blogeintrags – vor Einarbeitung der Änderungen, die sich aus den Kommentaren der Leser ergeben haben –, und sie dient als Sammlung für diejenigen Kommentare zum Haupttext, die ich dort nicht veröffentlicht habe, da sie der Schritt-für-Schritt-Erklärung vorgreifen oder in anderer Weise unkonstruktiv sind.
1. Vertiefungen zum Blogeintrag
[derzeit noch leer]
2. Originalversion des Blogeintrags
Ich habe bei meiner Schritt-für-Schritt-Einführung in die Spezielle Relativitätstheorie, “Einstein verstehen” (bislang erschienen: Teil 1, Teil 2) zwar bereits sehr elementar angefangen – mit Absicht, denn diese Einführung soll ja auch Leser mitnehmen, die nicht über weitergehendes physikalisches Vorwissen verfügen. In den Kommentaren kamen dann allerdings Fragen auf, die noch eine Ebene tiefer liegen und sich folgendermaßen zusammenfassen lassen: Was ist eigentlich eine gute Definition für eine Maßeinheit? Da ich das Thema spannend finde und es sich, wenn schon nicht als Hauptbeitrag, so doch als nützlicher Ergänzungstext für “Einstein verstehen” eignet, will ich der Frage hier nachgehen.
Einheiten
Vielleicht die wichtigste Eigenschaft der Naturwissenschaften ist, dass so viele ihrer Aussagen quantitativ formuliert werden können. Dazu benötigt man gut definierte Einheiten, denn messen heißt, mit einer Einheit zu vergleichen. Dass Usain Bolt 2009 in Berlin die 100 Meter in 9,58 Sekunden gelaufen ist, bedeutet, dass die Dauer seines Sprints das 9,58fache der im Internationalen Einheitensystem (Système International d’unités, daher abgekürzt zu SI) definierten Einheit “Sekunde” betrug. Wenn wir von Situationen absehen, in denen schlicht abgezählt wird, dann gibt es ohne Einheit keine Möglichkeit, quantitative Aussagen zu treffen.
Aber was ist eine “gute Maßeinheit”? Was heißt in diesem Zusammenhang “gut” oder, anders ausgedrückt: Welche Eigenschaften sind bei einer Einheitendefinition wünschenswert? Das ist die Schlüsselfrage der Metrologie, der Wissenschaft vom Messen und von den Maßeinheiten.
Konstanz und Reproduzierbarkeit
Entscheidende Eigenschaft einer Einheit ist, dass sie bezüglich der zu messenden physikalischen Größe konstant ist: Eine Längeneinheit muss eine konstante Länge haben, eine Zeiteinheit eine konstante Zeitdauer, eine Masseeinheit eine konstante Masse, und so weiter. Ansonsten würde es gar keinen Sinn ergeben, etwa von einer Länge von “1,2 Metern” zu reden; man müsste dann immer dazu sagen, wann und unter welchen Umständen die Messung durchgeführt wurde, und die allgemeine Vergleichbarkeit, die doch gerade den entscheidenden Nutzen von Maßeinheiten ausmacht, wäre nicht mehr gegeben.
Auf den ersten Blick könnte man denken, die Konstanz einer Einheit stelle sich automatisch ein, sobald man die Definition einmal getroffen hat. Schließlich ist die Einheit das Bezugsmaß, mit dem die betreffende Größe überhaupt erst gemessen wird. Ein Meter ist trivialerweise zu jedem Zeitpunkt einen Meter lang. Spätestens auf den zweiten Blick wird dagegen klar, dass es um etwas anderes geht.
Nehmen wir als Beispiel die letzte Maßeinheit des Internationalen Systems (SI), die noch durch ein bestimmtes Objekt, in der Sprache der Metrologie eine “Maßverkörperung” bzw. einen “Referenzkörper”, definiert wird: das Kilogramm. Die Masse “1 Kilogramm” ist die Masse des im Internationalen Büro für Maß und Gewicht in Paris aufbewahrten Urkilogramms, eines Zylinders aus einer Platin-Iridium-Legierung.
Verändert sich die Masse des Urkilogramms mit der Zeit? Logischerweise hat das Urkilogramm zu jedem Zeitpunkt genau so viel Masse wie es selbst, in diesem Sinne also: eine Masse von einem Kilogramm. Doch die Frage danach, ob sich die Masse des Urkilogramms verändert, ist ja eine etwas andere: Wenn wir das Urkilogramm jetzt und das Urkilogramm, wie es vor einem Jahr war, zusammen auf die Waage legen könnten, würde sich dann ein Unterschied zeigen? Direkt können wir diese Frage nicht beantworten – wir können schließlich schwerlich eine Zeitreise machen, um das Urkilogramm zu einem direkten Vergleich mit einer früheren oder einer zukünftigen Version seiner selbst heran zu holen.
Wir können allerdings ausnutzen, dass es Zwillinge des Urkilogramms gibt, zum einen solche, die genau so konstruiert sind wie das Urkilogramm, zum anderen solche, die aus anderen Materialien bestehen bzw. eine andere Form haben, aber ebenfalls konstante Masse besitzen sollten. Viele Nationen besitzen eigene Kilogramm-Exemplare als Grundlage der Massenbestimmung im eigenen Land; diese nationalen Exemplare reisen in unregelmäßigen Abständen nach Paris, um mit dem Urkilogramm verglichen zu werden. Sowohl das internationale Büro in Paris wie auch die nationalen Metrologie-Institute besitzen Sammlungen weiterer 1-Kilogramm-Objekte. (Soweit ich weiss, werden die Kilogrammkopien nicht nachträglich verändert; nach einer Vergleichsmessung wird lediglich notiert, um wieviele Bruchteile der Vergleichskörper vom Urkilogramm abweicht; kennt man diesen Zahlenwert, dann lässt sich aus dem Kilogramm-Objekt die genaue Masse “1 kg” rekonstruieren.)
Die Massen des Urkilogramms und seiner diversen Kopien kann man mit Hilfe von Präzisionswaagen miteinander vergleichen. Die beste Prototypwaage der Physikalisch-Technischen Bundesanstalt – des nationalen Metrologie-Instituts für Deutschland – kann Kilogrammmassen mit einer Genauigkeit von weniger als 0,2 Millionstel Gramm vergleichen. Das entspricht einer relativen Genauigkeit von stolzen 0,2 Milliardsteln!
Zeigen sich bei diesen Vergleichsmessungen Abweichungen, dann könnte es natürlich im Prinzip sein, dass das Urkilogramm vollkommen unverändert geblieben ist, aber die verschiedenen Kopien z.B. ein paar Atome verloren oder dazugewonnen haben. Andererseits: Die physikalischen Eigenschaften eines Metallzylinders werden sich kaum ändern, nur weil er per internationalem Dekret zum Urkilogramm erklärt wurde. Man muss daher davon ausgehen, dass das Urkilogramm genau so Masse verliert oder gewinnt wie baugleiche Objekte, die unter vergleichbaren Bedingungen aufbewahrt werden.
In der folgenden Grafik sind Massenänderungen verschiedener Urkilogramm-Kopien relativ zum Urkilogramm aufgetragen, die sich bei verschiedenen Vergleichsmessungen seit 1889 ergeben haben und von denen die Forscher bislang noch nicht wissen, wie sie zustandekommen:
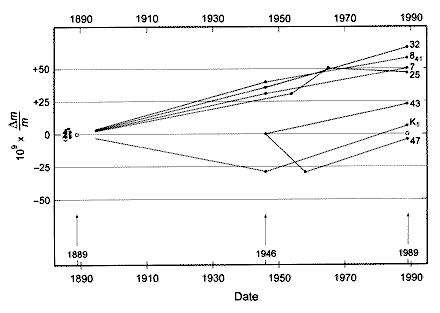 [Bild: BIPM-Webportal, Seite Verifications, abgerufen am 27.5.2011.]
[Bild: BIPM-Webportal, Seite Verifications, abgerufen am 27.5.2011.]
Vorsichtiger Weise sollte man davon ausgehen, dass sich die Masse des Urkilogramms mit der Zeit mindestens um einen Betrag verändert, der von derselben Größenordnung ist wie die Abweichungen, die sich beim Vergleich der Vergleichsobjekte untereinander und mit dem Urkilogramm zeigen. Aus solchen Vergleichsmessungen, im Fachjargon auch “Typ A-Messungen” genannt, lässt sich die Größenordnung der Veränderungen, mit denen man für das Urkilogramm rechnen sollte, abschätzen.
Bei Maßeinheiten, die nicht über einen künstlichen Referenzkörper definiert sind, kann man analog vorgehen. Bei einer früheren Definition der Sekunde mit Hilfe der Erdrotation beispielsweise nutzten die Astronomen die periodische Bewegung des Mondes um die Erde und der Planeten um die Sonne zu Vergleichsmessungen – und erhielten so tatsächlich Hinweise darauf, dass es ihrer gewählten Einheitendefinition an Konstanz mangelte!
Moderne Maßeinheiten wie Sekunde und Meter sind über die Eigenschaften von Licht definiert, das bei genau definierten Prozessen von bestimmten Atomsorten ausgesandt wird; eine Ergänzung, wie die Definition in die Praxis umzusetzen ist (ein “mise en pratique”) legt alle relevanten näheren Umstände des Experiments fest. So kann jedes hinreichend gut ausgerüstete Labor mit Hilfe geeigneter Experimente die Länge der Sekunde und des Meters rekonstruieren.
An die Stelle der Vergleiche verschiedener Referenzkörper tritt in diesem Falle der Vergleich unterschiedlicher Versionen des zur Definition verwandten Experiments, sei es innerhalb eines Labors, sei es zwischen verschiedenen Laboren: die genaue Reproduzierbarkeit der Maßeinheit.
Verstehbarkeit, Kontrollierbarkeit, Erforschbarkeit
Die erwähnten Vergleichsmessungen eines Referenzkörpers wie des Urkilogramms und seiner Kopien erlauben Rückschlüsse darauf, dass sich solche Körper ändern. Je nach Art der Änderung kann es allerdings durchaus sein, dass Vergleichsmessungen nur einen kleinen Teil der Änderungen anzeigen, die dort tatsächlich stattfinden. Angenommen, es handle sich um einen systematischen Prozess, in dem die betreffenden Kilogrammkörper sämtlich Masse verlieren, und zwar einige etwas schneller, andere etwas langsamer. Dann könnte die Vergleichsmessung lediglich nachweisen, dass der Masseverlust bei einigen der Körper etwas schneller, bei anderen etwas langsamer vor sich geht. Wieviel Masse diese Körper insgesamt verlören, bliebe den Vergleichen dagegen verborgen.
Anders gesagt: Wenn das Urkilogramm und seine Kopien alle pro Jahrzehnt jeweils 10 Tausendstel Gramm an Materie verlören (eine komplett fiktives Zahlenbeispiel), dann könnte kein Vergleich dieser Körper untereinander diesen Umstand nachweisen. Der Vergleich würde immer nur zeigen, dass jeder der Körper nach wie vor die gleiche Masse hätte wie die anderen.
Weitergehende Aussagen können wir nur machen, wenn wir verstehen, was da vorgeht. Bereits ein ungefähres Verständnis kann weiterhelfen – ein Beispiel sind Verunreinigungen, die sich trotz aller Vorsichtsmaßnahmen auf dem Urkilogramm und seinen Kopien ansetzen und deren Masse vergrößern. Was da vorgeht, lässt sich verstehen, wenn man das Gewicht von Urkilogrammkopien vor und nach einer bestimmten Reinigungsprozedur vergleicht:
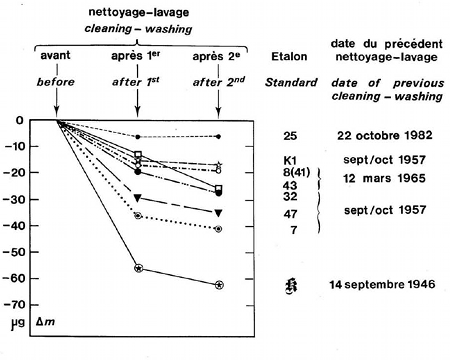 [Bild: Abb. 15 aus G. Girard, The Washing and Cleaning of Kilogram Prototypes at the BIPM, BIMP 1990]
[Bild: Abb. 15 aus G. Girard, The Washing and Cleaning of Kilogram Prototypes at the BIPM, BIMP 1990]
Jede Kurve steht dabei für einen Urkilogramm-Zwilling; die Objekte sind rechts am Rand identifiziert (25, K1 usw.). Angegeben ist jeweils der Massenverlust in Millionstel Gramm (Mikrogramm, µg) nach dem ersten und dem zweiten Reinigungsschritt. Die Reinigungen wurden zu Beginn des dritten Abgleichs des Urkilogramms mit den nationalen Referenzkopien vorgenommen (der Abgleich fand von 1989 bis 1992 statt). Ganz rechts steht für jeden der Körper, wann er zuvor das letzte Mal gereinigt worden war.
Offenbar verlieren die Kilogrammkopien beim Reinigen an Masse; wie zu erwarten im ersten Reinigungsschritt mehr als im zweiten. Außerdem ist der Masseverlust umso größer, je mehr Zeit seit der letzten Reinigung vergangen ist. Am meisten Masse hat beim Reinigen das Urkilogramm (Frakturbuchstabe k) verloren, das zuletzt beim vorangehenden derartigen internationalen Vergleich 1946 gereinigt worden war.
Diese Zusammenhänge zeigen an, was dort vor sich geht: An den Kilogramm-Körpern lagern sich Verunreinigungen ab; die Ablagerungsraten kann man aus der obigen Grafik abschätzen. Durch Reinigen lassen sich die Ablagerungen weitgehend entfernen. Ist der Effekt einigermaßen verstanden, kann man ihn berücksichtigen, in diesem Falle: Sollen Abweichungen von weniger als einigen Dutzend Mikrogramm ausgeschlossen werden, dann reinigen die Metrologen die Kilogrammkörper vor dem Vergleichen, einer genau festgelegten Prozedur folgend.
Das Beispiel zeigt eine weitere Eigenschaft guter Maßeinheiten: Sie sollten so definiert sein, dass die betreffenden Wissenschaftler die so definierte Einheit und mögliche Störeinflüsse möglichst genau verstehen. Das Beispiel zeigt allerdings auch, dass ein konkretes Referenzobjekt es erschwert, Störeinflüsse und Variationen gezielt und systematisch zu erforschen. Das Objekt soll ja so ungestört und unbeeinflusst aufbewahrt werden wie möglich. Unter diesen Bedingungen ist es noch nicht einmal möglich, eine winzige Materialprobe zu nehmen und zu untersuchen!
Sind die Störeinflüsse bekannt, dann wird man selbstverständlich alles so einzurichten versuchen, dass die Einheitendefinition davon so weit wie irgend möglich unbeeinflusst bleibt.
Beim Prototyp für die (inzwischen veraltete) Definition des Meters beispielsweise, dem Urmeter, wurde der Querschnitt so gewählt, dass sich der Stab beim Messvorgang möglichst wenig in sich verdrehen kann; die Legierung, 90% Platin und 10% Iridium, wurde nach den Kriterien hoher Härte und Korrosionsbeständigkeit und geringer Elastizität gewählt. (Das Ausdehnungsverhalten bei verschiedenen Temperaturen spielte bei der Materialwahl keine wichtige Rolle; stattdessen hat man eine Ablesetemperatur festgeelgt: 0 Grad Celsius.)
Die Definitionen von Maßeinheiten mit Hilfe von Laborexperimenten und die ergänzenden Durchführungsbestimmungen “mise en pratique” werden ebenfalls so gewählt, dass alle bekannten Störeinflüsse so weit wie möglich unterdrückt werden; gibt es an irgendeiner Stelle Auswahlmöglichkeiten, wie eine bestimmte Messung durchgeführt werden kann, wird man immer dasjenige Verfahren empfehlen, das am wenigsten anfällig gegenüber Störungen ist und die genaueste Reproduzierbarkeit verspricht.
Verfügbarkeit
Maßeinheiten sind nur dann nützlich, wenn sie möglichst allgemein zugänglich sind. Sie sollen ja gerade Vergleichbarkeit sicherstellen – die Physiker in Hamburg sollen Ergebnisse Ihrer Experimente, die sie mit Hilfe von Maßeinheiten ausgedrückt haben, ohne Schwierigkeit mit den Ergebnissen der Kollegen in Boston vergleichen können, und ein über Maßeinheiten festgelegter Standard soll dazu führen, dass die CD-Spieler-Hersteller in China CD-Spieler herstellen können, auf denen sich in Japan gebrannte CDs abspielen lassen.
Frühe Längeneinheiten waren zumindest näherungsweise so definiert, dass jedermann sie ohne großen Aufwand nachvollziehen konnte: die Elle, definiert über die Länge eines Unterarms, ist zumindest grob für jeden Menschen anhand seines eigenen Körpers nachvollziehbar; gleiches gilt für die (Hand-)Spanne oder den Fuss.
Allerdings war das natürlich keine sehr genaue Definition, da Körpermaße von Mensch zu Mensch gehörig variieren; beim Zoll wurde stattdessen versucht, die Definition zu präzisieren als die durch drei hintereinander gelegte Gersternkörner definierte Länge, wobei jedes der Gerstenkörner rund und trocken zu sein habe. Immer mehr setzten sich dann allerdings konkrete Referenzkörper durch; Kopien davon konnte man hinreichend allgemein zugänglich machen, indem man sie beispielsweise an öffentlichen Orten aufhing:

[Bild: M. Schweiss. Gefunden auf Wikimedia Commons]
Mit Vereinheitlichung der Maße wurden die Referenzkörper allerdings immer weniger gut zugänglich, denn zumindest das Original ist ja jeweils nur an einem einzigen Ort untergebracht. Ist es aus irgendwelchen Gründen nicht zugänglich, so haben die Metrologen ein Problem. Beispielsweise kam einem der internationalen Vergleiche des Urkilogramms mit seinen Kopien der II. Weltkrieg in die Quere.
Definitionen, die auf Naturgesetzen und Naturkonstanten beruhen, etwa die erwähnten Definitionen von Meter und Sekunde mit Hilfe der Eigenschaften von Licht, vereinen hohe Verfügbarkeit mit hoher Präzision. Sie sind für jedes hinreichend gut ausgestattete Physiklabor direkt reproduzierbar – ein weiterer großer Vorteil dieser Art von Definition.
Beständigkeit
Sicher, es ist sehr unwahrscheinlich, dass ein Flugzeug auf das Internationale Büro für Maße und Gewichte stürzt, oder dass eine andere Katastrophe das Urkilogramm beschädigt. Und selbst wenn, dann sollte es gelingen, diese Masse mit Hilfe der existierenden Kopien ungefähr zu rekonstruieren. Dennoch dürfte den meisten Metrologen auch im Hinblick auf die Robustheit und Beständigkeit nicht ganz wohl dabei sein, eine Maßeinheit an ein bestimmtes Objekt zu binden.
Hier können Definitionen, die auf Naturgesetzen und Naturkonstanten beruhen, einmal mehr punkten. Solange unsere wissenschaftliche Tradition nicht durch eine weltweite Katastrophe komplett unterbrochen wird, werden uns Maßeinheiten, die jedes hinreichend ausgerüstete Laboratorium reproduzieren kann, erhalten bleiben.
Technische Anforderungen
 Allein schon aus Gründen grundlagenforscherischen Ehrgeizes streben Metrologen nach immer höherer Präzision. Doch auch bei technischen Anwendungen geht der Trend hin zu immer höherer Genauigkeit. Dass Satellitennavigationssysteme heute auf Genauigkeiten von einigen Milliardstel Sekunden angewiesen sind, oder dass industrielle Standards für in jedem Haushalt verfügbare Massenware wie CDs für bestimmte Größen Genauigkeiten von Zehnmillionstel Metern vorgeben werden (z.B. 11.3 im ECMA-Standard 130) dürfte sich vor hundert Jahren noch niemand träumen gelassen haben. Klar ist, dass jede Einheit mindestens so genau definiert sein muss, wie es die Anwendungen in Alltag, Industrie und Handel (vgl. z.B. den Kaarls-Report) erfordern. Und die erwähnten Beispiele GPS und CD/DVD zeigen, dass es sich lohnen kann, die Präzision vorausschauend noch merklich höher zu wählen.
Allein schon aus Gründen grundlagenforscherischen Ehrgeizes streben Metrologen nach immer höherer Präzision. Doch auch bei technischen Anwendungen geht der Trend hin zu immer höherer Genauigkeit. Dass Satellitennavigationssysteme heute auf Genauigkeiten von einigen Milliardstel Sekunden angewiesen sind, oder dass industrielle Standards für in jedem Haushalt verfügbare Massenware wie CDs für bestimmte Größen Genauigkeiten von Zehnmillionstel Metern vorgeben werden (z.B. 11.3 im ECMA-Standard 130) dürfte sich vor hundert Jahren noch niemand träumen gelassen haben. Klar ist, dass jede Einheit mindestens so genau definiert sein muss, wie es die Anwendungen in Alltag, Industrie und Handel (vgl. z.B. den Kaarls-Report) erfordern. Und die erwähnten Beispiele GPS und CD/DVD zeigen, dass es sich lohnen kann, die Präzision vorausschauend noch merklich höher zu wählen.
Einfache Messpraxis
Bei allen Anforderungen an die Präzision gilt: Je weniger aufwändig es ist, mit Hilfe der Maßeinheit konkrete Messungen durchzuführen, umso günstiger. Bei der von 1956 bis 1967 gültigen Definition der Sekunde, die die Mondbewegung als natürliche Uhr heranzog, dauerte es rund fünf Jahre, um die Maßeinheit Sekunde alleine aufgrund von Beobachtungen des Mondes mit hinreichender Genauigkeit zu rekonstruieren. Die moderne Definition der Sekunde anhand von Laborexperimenten erreicht binnen Minuten eine größere Genauigkeit.
Dass die Messung durch Fachleute mit entsprechender Ausrüstung durchgeführt werden muss, dürfte, wenn es um Präzisionsmessungen gibt, unvermeidlich sein; nur sollte man es zumindest diesen Fachleuten so einfach wie möglich machen.
Definitionen mit Hilfe von Naturgesetzen und Naturkonstanten
All diese Anforderungen zusammen haben in den letzte Jahrzehnten zu einem eindeutigen Trend bei der Definition von Maßeinheiten geführt. Möglichst einfache Situationen herzustellen, möglichst einfache Systeme zu präparieren, deren grundlegende Eigenschaften möglichst vollständig zu beschreiben und alle Störeinflüsse soweit wie möglich auszuschließen – das ist die Arbeitsweise der Experimentalphysik (und anderer experimenteller Wissenschaften).
Aus entsprechenden Experimenten und ihrer theoretischen Beschreibung hat sich das moderne physikalische Bild der Welt entwickelt, mit grundlegenden Naturgesetzen, die sich in der Sprache der Mathematik formulieren lassen. Vielleicht die wichtigste physikalische Erkenntnis ist, dass die Materie, mit der wir es hier auf der Erde zu tun haben, die wir im Alltag und in der Industrie verwenden, ebenso wie die Materie, deren Licht wir aus den Tiefen des Alls auffangen, aus Atomen besteht. Die Atome wiederum bestehen aus Elementarteilchen: ihre Kerne aus Neutronen und Protonen, ihre Hüllen aus Elektronen. Atome, Atomsysteme und ihre Eigenschaften sind in unzähligen Experimenten hochpräzise erforscht worden – von der Grundlagenforschung bis hin zu vielfältigen Anwendungen wie Transistoren und Laser.
Die Erforschung der grundlegenden Eigenschaften der Materie hat auch gezeigt, welche einfachen Materiesysteme für die genaue Definition von Maßeinheiten besonders geeignet sind. Die Wellenlängen eng definierter Frequenz beispielsweise, die Atome bei so genannten Spektrallinien aussenden, werden direkt durch einfache Eigenschaften des Atoms bestimmt – die Anzahl von Neutronen, Protonen und Elektronen, aus denen das Atom besteht –, wie sie von äußeren Umständen (z.B. äußeren Magnetfeldern) abhängen, ist gut erforscht, die äußeren Umstände sind gut kontrollierbar, und es sind hochpräzise Verfahren bekannt, diese Wellenlängen zu messen.
Ein Prototyp aus Metall ist im Vergleich mit einfachen Atomsystemen ein hochkomplexes Gebilde: Eine Legierung, also Gemisch aus einer Vielzahl von Atomen, wobei nicht exakt bekannt ist, in welcher Zahl welche Isotope (sprich: welche Atome mit einer bestimmten Neutronen- und Protonenzahl im Atomkern) darin vertreten sind; die Atome sind typischer Weise zu kleinen Kristallen zusammengesetzt, die sich wiederum in unübersichtlicher Weise zum eigentlichen Festkörper verbinden; zusätzlich können noch weitere Moleküle, z.B. von Gasen, im Festkörper eingeschlossen sein. All das macht z.B. das Urkilogramm zu einem nur schwer kontrollierbaren Objekt. Könnte es sein, dass darin eingeschlossene Gase mit der Zeit aus dem Festkörper entkommen? Rührt von solchen oder ähnlichen Effekten die relativ zu den meisten Urkilogramm-Kopien schrumpfende Masse (s.o.) her?
Konstanz bzw. Reproduzierbarkeit, daraus abgeleitete Kriterien wie Verstehbarkeit und Kontrollierbarkeit, um Störeinflüsse einschätzen und vermeiden zu können, Verfügbarkeit, Robustheit, den technischen Anforderungen genügbare Genauigkeit und dabei doch möglichst einfache Messpraxis – das haben wir als Wunschzettel für eine gute Einheitendefinition herausgearbeitet, und an diesen Kriterien orientiert hat die für die Definition von Maßeinheiten zuständige internationale Konferenz, die Generalkonferenz für Maß und Gewicht, mittlerweile so gut wie alle Definitionen des internationalen Einheitensystems an einfache physikalische Systeme geknüpft, deren Eigenschaften idealerweise nur von den Naturgesetzen und Naturkonstanten abhängen.
Jedem Wechsel von einer alten zu einer neuen Definition sind dabei jahrelange Tests vorausgegangen; eine neue Definition wurde jeweils nur eingeführt, wenn sichergestellt war, dass sie im Rahmen der mit der alten Definition erreichbaren Genauigkeit mit der alten Definition übereinstimmte. Wie schon erwähnt ist die letzte Definition, die noch an ein konkretes Objekt gebunden ist, das Kilogramm. Aber es ist zu erwarten, dass sich auch das in naher Zukunft ändert: Noch 2011 tagt die nächste Generalkonferenz, und es ist zu erwarten, dass sie die eine neue Definition des Kilogramms einführt, die dann ebenso nur noch von Naturgesetzen und Naturkonstanten abhängt.
Wie die Entwicklung der Definitionen für die grundlegenden Einheiten verlaufen ist, ist eine Geschichte für sich; die verdient dann aber einen eigenen Blogbeitrag.
3. Nicht auf der Hauptseite veröffentlichte Kommentare
[derzeit noch leer]

